摩杰注册

现有各种智能优化算法（比如遗传算法，粒子群算法等）。经常看到建议“根据问题选择算法”。想请教一下“根据问题选择算法”的基本思路是什么样的？

智能优化算法是一类基于概率的随机搜索进化算法，各个算法之间存在结构、研究内容、计算方法等具有较大的相似性。因此，群体智能优化算法可以建立一个基本的理论框架模式：

Step1：设置参数，初始化种群；

Step2：生成一组解，计算其适应值；

Step3：由个体最有适应着，通过比较得到群体最优适应值；

Step4：判断终止条件示否满足？如果满足，结束迭代；否则，转向Step2；

各个群体智能算法之间最大不同在于算法更新规则上，有基于模拟群居生物运动步长更新的（如PSO，AFSA与SFLA），也有根据某种算法机理设置更新规则（如ACO）。

可以考虑试试最新的群智能优化算法:蜣螂优化算法，亲测效果不错

完整的数学原理和代码详细讲解视频（时长30分钟左右）地址：基于Matlab的海鸥优化算法（SOA）对23种测试函数的代码和数学原理详细讲解视频（全网最全）_哔哩哔哩_bilibili

完整的Matlab代码（含说明文档）的提取地址： 正在为您运送作品详情

来源：

海鸥优化算法是印度学者Gaurav Dhiman于2018年提出的一种受生物启发的智能优化算法，该算法的主要灵感来自于自然界中海鸥的迁徙和攻击行为，这些行为经过数学建模和实现，可以在给定搜索空间中进行探索和利用。

生物学原理：

一般来说，海鸥是群居性的，它们用自己的智慧来寻找并攻击猎物。海鸥最重要的是它们的迁徙和攻击行为。迁徙被定义为海鸥从一个地方到另一个地方的季节性迁移，以寻找最丰富食物来源，以提供足够的能量。该行为可描述为：

在迁徙过程中，它们成群结队地迁徙。海鸥的初始位置不同，以避免相互碰撞；在一个群体中，海鸥可以朝着最适合生存的海鸥的方向前进；其他海鸥可以根据最适合的海鸥更新它们的初始位置。海鸥在迁徙过程中，会经常攻击其他候鸟，在攻击过程中，它们可以做出螺旋形的自然运动，如图1所示。

图1

数学原理：

迁徙（探索）：

在迁移过程中，海鸥优化算法模拟了海鸥群如何向一个位置移动到另一个位置。在这个阶段，海鸥应该满足三个条件:

1.避免碰撞：为了避免与邻居(即其他海鸥)的碰撞，引入了额外的变量A ,用于计算新搜索代理的位置，公式如下：

其中，

表示与其他搜索代理不发生碰撞的搜索代理的位置，

表示搜索代理的当前位置，t表示当前迭代次数，A表示给定搜索空间中搜索代理的移动行为。

上述等式中fc为引入的控制A的频率参数，类似于其他智能算法的权重，使得A从fc的值线性递减到0；fc设置为2可以调整。

2.朝最优的邻居方向移动：在邻居避免碰撞之后，搜索代理朝着最优邻居的方向移动,如公式3所示：

上述公式中Ms为最佳位置Pbest和搜索位置X的相对位置，B模拟海鸥的随机行为：

3.靠近最优位置进行搜索：根据最优搜索位置，每只海鸥更新位置，公式如下：

飞行

海鸥在迁徙过程中可以不断改变攻击角度和速度，并利用翅膀和重量来保持高度。当攻击猎物时，会在空中形成螺旋运动，抽象到x,y,z平面：

上述公式中的u，v就是定义螺旋状态的常量，这个和鲸鱼优化算法（WOA）是非常相似的。

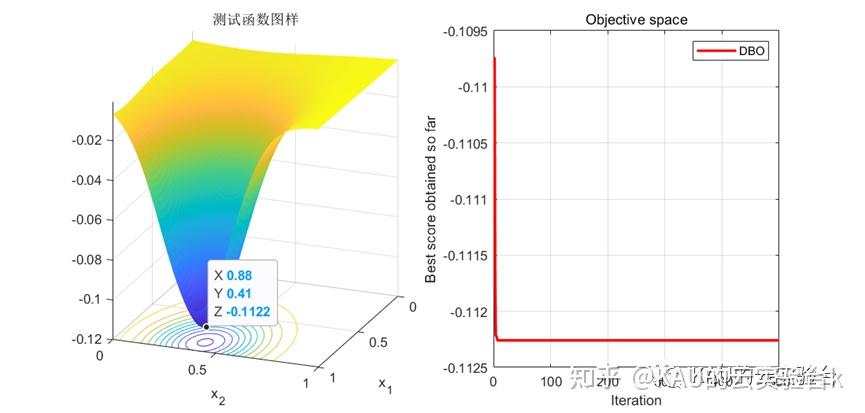
蜣螂优化算法(dung beetle optimizer，DBO)是JiankaXue 和Bo Shen在2022 年提出的一种新型群体智能优化算法[1]，其灵感来自于蜣螂的滚球、跳舞、觅食、偷窃和繁殖行为。该算法同时考虑了全局探索和局部开发，从而具有收敛速度快和准确率高的特点，可以有效地解决复杂的寻优问题。本文将对该算法进行原理讲解及程序实现。

00 文章目录

1 蜣螂优化算法原理

2 代码目录

3 算法性能

4 总结

01 蜣螂优化算法原理

自然界中，蜣螂的特点是将粪便滚成球，利用天体线索导航，从而使球沿直线滚动。然而，没有任何光源，屎壳郎的路径就不再是直线了。此外，许多自然因素也会导致屎壳郎偏离原来的方向。再者，屎壳郎可以通过舞蹈来重新确立自己的方向。粪球还可以作为虫卵的繁殖地。除此之外，还有一种偷窃行为，一些蜣螂会把食物作为自己的食物来竞争。

在DBO中，每只蜣螂的位置对应一个解。蜣螂觅食时的行为有五种:滚球，即把粪便滚成一个球，利用天体线索进行导航，从而把球滚成一条直线;跳舞，这让蜣螂重新定位自己;觅食，一些成年蜣螂会从地下钻出来寻找食物;偷窃，一些被称为小偷的蜣螂会从其他蜣螂那里偷取粪球;繁殖，在自然界中，蜣螂会把粪球滚到安全的地方，藏起来进行繁殖。

因此算法中蜣螂种群分为四个部分，分别为滚球蜣螂、育雏球、小蜣螂和小偷蜣螂。滚球蜣螂受各种自然环境影响决更新其运行方向，初步寻找可以安全觅食的位置，育雏球会被产在已知的安全区域内，成长为成虫的蜣螂被称为小蜣螂，小蜣螂会在最佳觅食区觅食，小偷蜣螂也会根据其他蜣螂的位置和最佳觅食区寻找食物。

四种蜣螂位置更新方式如下：

(1)滚球蜣螂

滚球蜣螂以太阳为导航以保证粪球在直线路径上滚动，光源强度、风等自然因素会影响滚球蜣螂的行进路线，

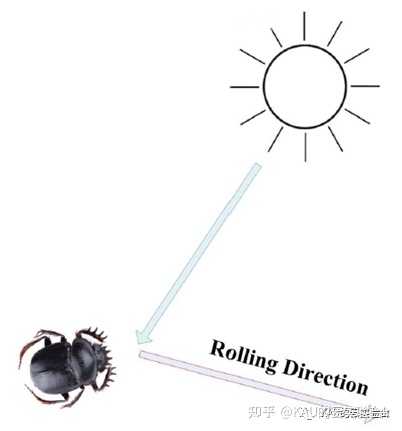
图源文献[1]

滚球蜣螂位置更新方式如下：

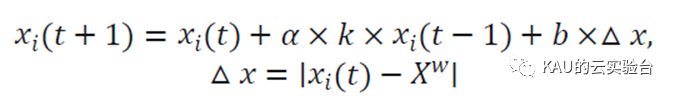
式中， 代表当前迭代次数， ( )表示第 次迭代时第 只蜣螂的位置信息，α 是一个自然系数，表示是否偏离原来方向，根据概率法分配为?1或1， ∈ (0,0.2)表示偏转系数， ∈ (0,1)表示常数， 和 分别设定为0.1和0.3， 表示全局最差位置，Δ 用于模拟光强变化。

当蜣螂遇到障碍物而不能前进时，它需要通过跳舞来调整自己的方向，滚球蜣螂跳舞更新位置的公式定义如下：

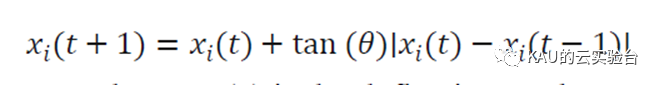
式中θ ∈[0, ]表示偏转角，在θ等于0、 /2或 时，蜣螂的位置不会更新。

(2)育雏球

育雏球采用边界选择策略模拟雌性蜣螂产卵区域，产卵区域的定义为:

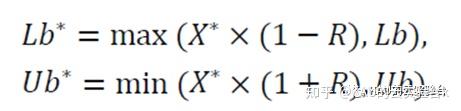
式中， ?表示当前的局部最佳位置， ?和 ?分别表示产卵区的下限和上限，=1 ? / ， 表示最大迭代数， 和 分别代表优化问题的下限和上限。

在迭代过程中，育雏球位置是动态变化的，其定义为：

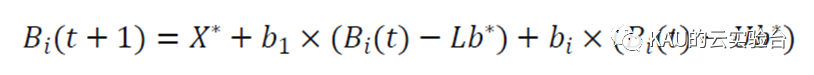
式中， ( )是第 次迭代时第 个育雏球的位置信息， 1和 2代表两个大小为1×D 的独立随机向量，D 表示优化问题的维度。

(3)小蜣螂

需要建立一个最优觅食区域，指导幼体蜣螂寻找食物并模拟其觅食行为，其中最优觅食区域定义为：

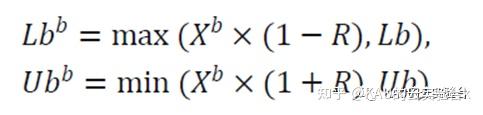
式中， b表示当前的局部最佳位置， b和 b分别表示最佳觅食区的下限和上限

小蜣螂的位置更新如下：

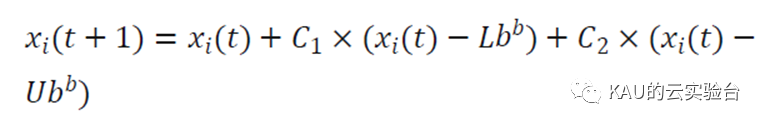
式中， ( )是第 次迭代时第 只小蜣螂的位置信息， 1表示遵循正态分布的随机数， 2 ∈(0,1)表示随机向量。

(4)小偷蜣螂

Xb是食物竞争的最佳位置，因此小偷蜣螂位置更新方式如下：

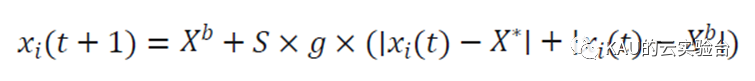
式中， ( )第 只小偷蜣螂在第 次迭代的位置信息，g 表示一个遵循正态分布的大小为1×D的随机向量，S表示一个常数值。

综上所述，DBO 算法主要分为六个步骤。

1）初始化蜣螂种群和DBO 算法的参数；

2）根据目标函数计算所有蜣螂位置的适度值；

3）更新所有蜣螂的位置；

4）判断每个更新后的蜣螂是否出了边界；

5）更新当前最优解及其适度值；

6）重复上述步骤，在 达到最大迭代次数后，输出全局最优值及其最优解。[2]

02 代码目录

代码注释完整，其中部分DBO程序如下：

代码获取方式见文末

03 算法性能

采用CEC的一个测试函数来初步检验其寻优性能，得到结果如下：

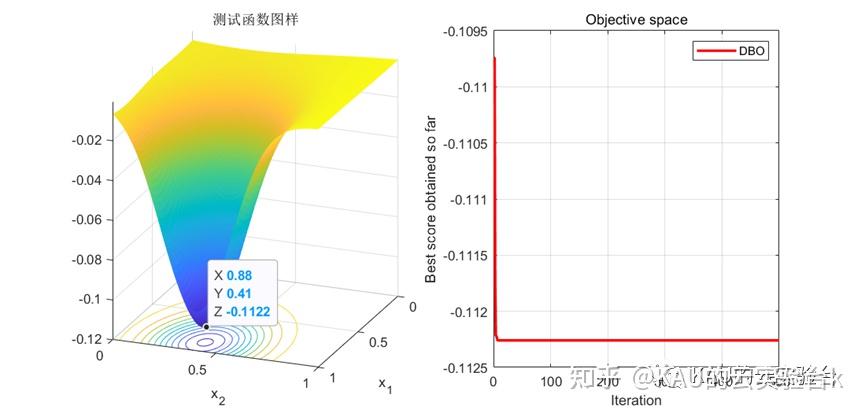
04 总结

本文介绍了蜣螂优化算法的原理及其MATLAB实现，蜣螂优化算法虽然具有寻优能力强，收敛速度快的特点，但同时也存在全局探索和局部开发能力不平衡，容易陷入局部最优，且全局探索能力较弱的缺点，因此作者将在后面的文章中继续介绍其改进方法。

参考文献

[1]Xue Jiankai, Shen Bo. Dung beetle optimizer: a new meta-heuristic algorithm for global optimization[J]. Journal of Supercomputing, 2023,79(7):7305-7336.

[2]潘志远,卜凡亮.基于蜣螂算法优化的DV-Hop定位算法[J/OL].电子测量与仪器学报:1-10[2023-08-16].http://43.138.60.40/kcms/detail/11.2488.TN.20230803.1820.026.html

蜣螂优化算法MATLAB源码获取：

在作者公众号 KAU的云实验台 回复: DBO (大写字母)

另：如果有伙伴有待解决的优化问题（各种领域都可），可以发我，我会选择性的更新利用优化算法解决这些问题的文章。

如果这篇文章对你有帮助或启发，可以点击右下角的赞/在看(?_)?(不点也行)

猎豹优化算法（The Cheetah Optimizer，CO）由MohammadAminAkbari等人于2022年提出，该算法性能高效，思路新颖。

参考文献： Akbari, M.A., Zare, M., Azizipanah-abarghooee, R. et al. The cheetah optimizer: a nature-inspired metaheuristic algorithm for large-scale optimization problems. Sci Rep 12, 10953 (2022). https://doi.org/10.1038/s41598-022-14338-z

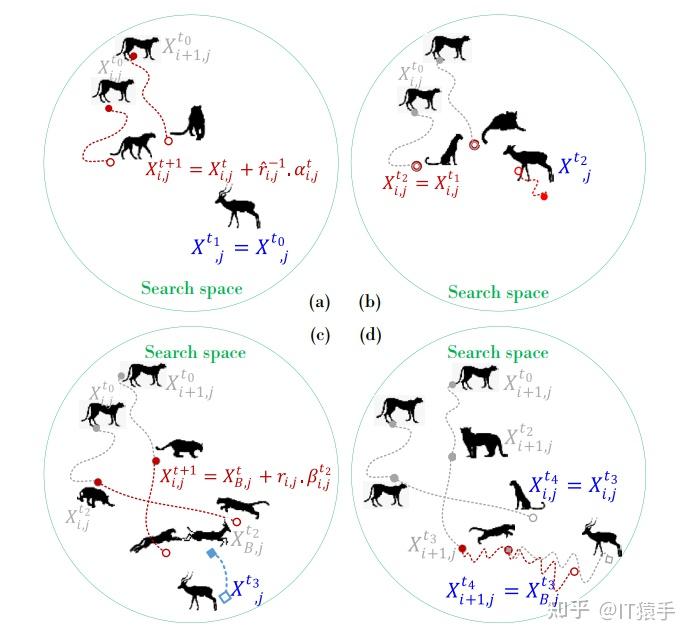
CO算法描述：

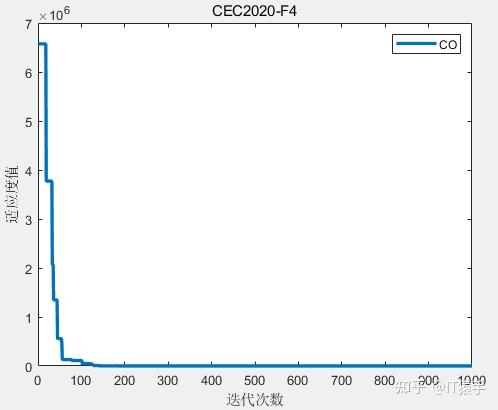
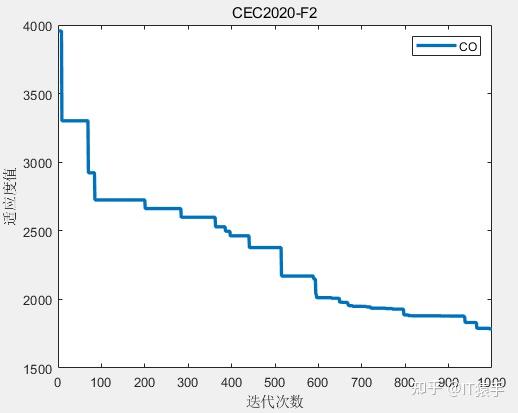
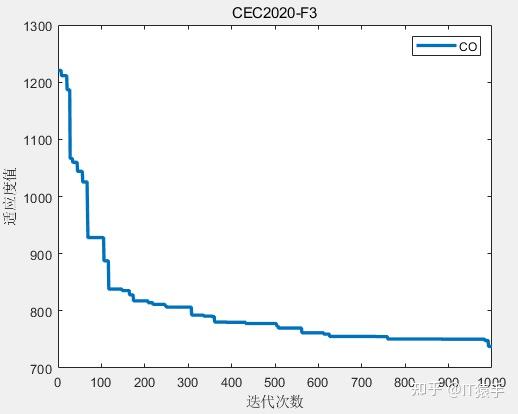
CEC2020共有10个测试函数测试维度包含：2D、5D、10D、15D、20D。CEC2020测试问题随着维度的增加求解极其困难。

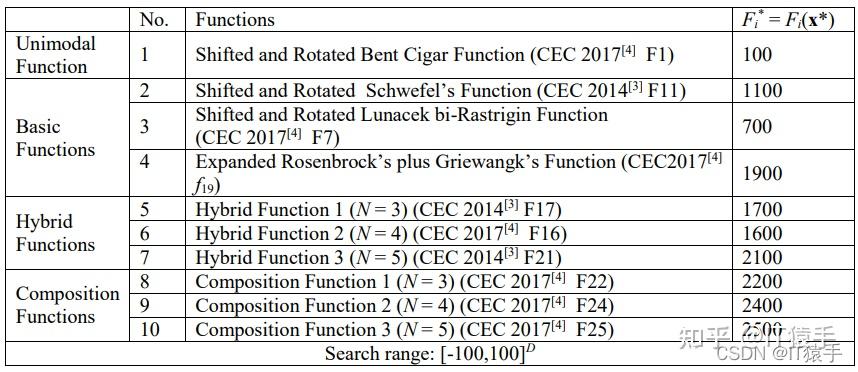
将猎豹优化算法CO运用于求解CEC2020中10个函数，其中每个测试函数可以选择的维度分别有：2D、5D、10D、15D、20D。增大迭代次数，CO的求解效果更佳。本例测试函数维度均为10D（可根据自己需求调整），种群大小为50，最大迭代次数为1000次。

close all
clear
clc
MaxFes=1000;%迭代次数
VarNumber=10;%维度 2/5/10/15/20
nPop=50;%种群大小
VarMin=-100;%下限
VarMax=100;%上限
fitnessfunc=str2func('cec20_func');
Function_name=1;
[Best_Fit,Best_Pos,Curve]=CO(nPop,MaxFes,VarMin,VarMax,VarNumber,CostFunction);  
figure
plot(Curve,'linewidth',2.5)
xlabel('迭代次数')
ylabel('适应度值')
legend('CO')
title(strcat('CEC2020-F',num2str(Function_name)))

部分结果如下：

F1:

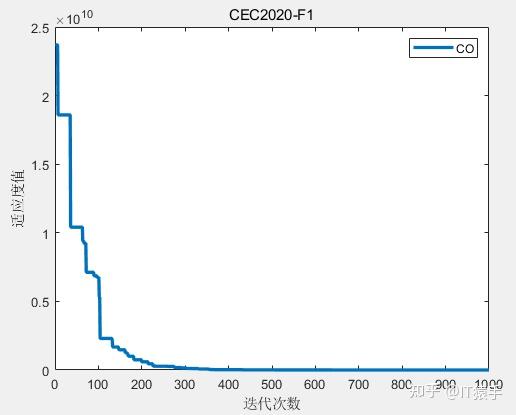
F2:

F3:

F4: