摩杰注册
每种语言都有自己擅长和不擅长的一面,语言本身特性再好也能被烂代码毁掉。世上99%的程序都轮不到比拼原生语言性能的地步。不同场景下,原生机器码未必比虚拟机runtime强(如题目中的Go和C#),甚至编译型写得不好还不如解释型(如IO密集场合)。
与其争论语言本身极端情况下的性能到底如何,倒不如把各个实际应用中的逻辑老老实实地写好吧。有的地方少加几个低效的循环,必要的地方用上缓存,数据库结构优化一下。提升的效率比Go和C#以及任何两门流行语言的性能差距大多了。另外如果以稍微牺牲一点性能的代价大大提升可读性和可维护性,也是十分值得的。
程序员要讲究格局和大势,不必拘于小节,主流编程语言的性能跟语言的地位基本是一致的,就是底层语言(汇编、C、C++..)> 中间层高级语言(Go,Java,C#...)> 上层脚本语言( Python,Lua,Ruby...)。知道这个大势就可以了,因为胎里素的原因,不会有错。
当然这是在同一水平程序员编程的情况下,如果程序员水平不一样,可能会出现底层语言性能不如高一层语言的情况,毕竟任何优化也拿烂代码没办法。明确这个大势,那么评估性能就变成,写出同样性能程序你要付出的代价要更值得权衡考虑。
一个程序设计语言的性能表现主要取决于编译器和运行时,以及代码质量。
谢邀。
利益相关:利益相关
最近看到了好多「华为方舟编译器」的帖子,
华为好棒,加油。
不过目前支付宝并未使用华为方舟编译器。
知道你们老吐槽说支付宝启动慢,
虽然能找出很多理由来解释,
比如支付宝通常不会常驻后台,
比如支付宝对安全更重视,启动时需要更仔细的检查等等。
但慢确实体验不好,再多的理由也没用。
所以近几年,我们悄悄启动了一个「秒开」的大项目。
这个事挺难的。
虽然我们有很多用户是用iPhone,用华为,
但还有更多的用户在用各种安卓系统
我们希望所有的用户,不管用什么手机,
不管是不是常驻后台,都能更快的享受服务。
这个难度可想而知。
一直没有官宣,
是因为我们觉得,虽然现在比以前快了不少,
但还没有达到我们的预期,
我们希望能让更多的人在使用时能「WOW」一下:
「启动秒开」、「扫码秒扫」、「切换秒滑」……
很开心已经有一些用户能直观感受到这种差别了。
既然被问到了,
还是说一下「秒开」背后的我们攻坚的技术,包括
容器框架原生化
虚拟机调优(profile-based compile)
线程调度管控
首页快照snapshot
扫码混合对焦
GPU运算
……
来都来了,
要是你是这方面的技术专家,
想让自己的技术造福全球超10亿用户,
来份简历呗~

作为专门优化数据库查询引擎的工程师,我对PostgreSQL的查询引擎稍微有点了解,勉强可以回答下这个问题。
先放结论:基于LLVM的JIT(codegen)在PostgreSQL中,并不是为了提升SQL解析的时间, 而是提升执行性能。对于大数据查询引擎(或者说OLAP)引擎来说, SQL解析的时间是几乎可以忽略不计的。关于JIT提升查询性能,目前我常用的有两个场景,一个是表达式优化,一个是消除冗余代码。
- 表达式优化
对于下面这段代码中的SQL,一个没有JIT查询引擎如何完成"a > 10 and b < 5"这样的操作呢?PostgreSQL的方案,是预先准备好大量的函数,函数有统一的接口,然后根据需要对函数进行拼接。
// 实例SQL
select count(*) from table where a > 10 and b < 5;
// PostgreSQL方案:多次函数调用
result = Int8AndOp(Int32GT(a, 10), Int32LT(b, 5));
// JIT方案:生成最小化底层代码
%res1 = icmp ugt i32 %a, 10;
%res2 = icmp ult i32 %b, 5;
%res = and i8 %res1, %res2;
比如a > 10这样的操作,PostgreSQL里面有很多求">"的函数,有求 int4和int8大小的,有求float4 和 float8大小的,根据需要找到响应的函数指针。所以,为了完成这个操作需要先调用一个函数求a > 10,然后调用一个函数求 b < 5, 最后在来一个求and的函数。为了完成这个表达式计算,需要3次函数调用。
但是使用LLVM的JIT, 只需要三行LLVM IR即可完成这一操作,翻译到底层汇编指令也是三行。三行汇编和三个函数调用所需要的执行时间差别是很大的,对于OLAP场景来说,因为要处理的数据多,性能差距更大。
2. 消除冗余代码
这块就比较玄学了。比如一行数据有三列,第一列是int4, 第二列是float4,第三列是个bpchar。但是程序员在谢数据库代码时候是不知道这些信息的。每次要处理某一列的时候,都需要检查下这一列的类型、长度、起始地址等信息。但是实际上在SQL写完以后,这些信息都有已经确定了。如果用LLVM生成代码,就可以在代码生成阶段引入这些信息。比如以前你需要在执行的时候判断这一列的类型,现在在LLVM JIT阶段已经知道了这个信息,这样最终生成的代码就不需要接续判断了。
数据库中有很多优化技术,都是对一些不起眼的角落进行优化,但是积少成多,最终的优化效果可能是很大的。
- GoDoc。 GoDoc的静态语言分析能力很强大,可以直接从代码和注释生成漂亮的文档。这一点区别于其他的类似工具如JavaDoc, PHPDoc或者JSDoc。这些工具需要添加额外的注解,比较麻烦。
- GoFmt。代码格式化一直是程序员编码的痛点,主要的困境在于没有统一的标准,Go通过内置的GoFmt工具来解决这个问题。
- GoLint。代码语法提示也在Go中通过GoLint工具进行了统一。
- 测试框架内置。这一点区别于其他的流行语言如Java, C#, Javascript,他们需要选择测试框架进行测试代码编写。而Go语言直接内置了测试框架,可以程序员快速生成测试框架代码,省时,省力。
- GoRoutines的并行化处理能力。Go对于并行化的支持做得非常彻底。直接把繁琐的线程创建封装起来,程序员无需担心线程创建中可能遭遇的硬件资源不足的问题。
- 使用Interface支持多态。在Go语言中省去了面向对象编程中父类继承的特征。在使用多态的地方使用Interface的模式实现多态,这样把代码结构线性化、平行化,从而降低了代码的复杂度。
1.异常和错误处理啰嗦。如果你习惯了使用异常处理,那么你就会很讨厌Go里面的错误处理方式。
- 你定义一个Go函数,返回一个错误;
- 调用这个函数时,你要判断返回错误是否为空;
- 然后判断是哪种错误
- 根据哪种错误进行相应的处理
- 这样的处理实在是啰嗦
2.空值判断。
- 在Go中指针类型可以是空,如果一个函数返回指针,在Go中,你需要进行上述第一条所说的啰嗦的错误处理,然后才可以使用指针。否则,如果这个指针为空,你使用它的话,会Crash。
3.作用域的限定比较另类。
- 大写字母开头可以全局访问,小写字母开头只能在当前文件可见。
- Go语言假定每个程序员都清楚the whole picture, 这在实际工作场景中是不现实的。
- 为了践行防御性编程理念,在Go中,不同程序员不得不创建大量的文件和目录。这样也不利于管理。
4.Go语言缺乏不可改写机制。
- 这是可能是因为它强调性能高于潜在的bug的规避。
5.Go语言缺乏泛型支持,我们不得不对潜在的数据类型进行转换。
6.Go语言缺乏继承机制,这导致共性功能的代码重用很难。
7.Go语言没有枚举类型,类似的功能不得不使用const,很不方便。
Go语言的应用场景主要集中在后端应用层和工具类开发,用来写单体服务,微服务以及工具。Go语言相对比较年轻,需要经过长时间的洗礼,大量的项目开发验证。目前来看,还无法与Java, C#这类语言的生态进行竞争。
综上,使用哪种语言是一种选择,适宜、简洁、高效、安全是核心。
根据客观事实和大家的评论,更新一个版本吧
release notes:
- 移除写的脑残的 C++
- java > go 修改为 java >=go
如果说性能的话,永远是 C=(写的不脑残的 C++) >> java >=go >> python
不过如果让我评价 go,除了某些特殊场合(简单的 io 和并发场景)写起来确实比较方便以外,大部分场合属实弟中弟,无论是语言设计还是开发效率
不信看看 k8s 社区搞了多少代码生成工具用来把 golang 糊成能用的样子
贴个 kubernetes member 的图,防止评论出现说我没用过 go 的精神小伙
Linalg dialect 是现在 MLIR-based ML 编译器中比较重要的一环,确实有很多有意思的设计和想法。我在日常工作中与其作者和主要贡献者都有比较频繁的交流,也给 Linalg dialect 提交过和审核过一些代码,在这里说一些自己的理解吧。不可能面面俱到,另外 Linalg dialect 正在飞快地发展中,很多东西可能很快就会过时,不过还是希望能给大家带来一些思考。
说到 Linalg dalect,难免需要涉及 MLIR 整个生态。看其他回答中大家似乎也是对 MLIR 生态本身更感兴趣一些。 不过在这里我并不打算长篇大论介绍 MLIR 的构想,而是想指出一些 MLIR 生态中常见的迷思和忽视的地方。了解这些也有助于比较客观地看待 MLIR 的现状以及其演进方向。
- MLIR core 本身只是提供一套定义编译器 IR 和撰写编译器 transformation 的基础工具。ML 编译器确实是 MLIR 想支持的很大的应用场景,也是 MLIR 开发的初衷,但是从 MLIR 脱离 TensorFlow 变为 LLVM project 的一个子项目之后,它基本就是一个比较中立的基础工具了。还有其他的完全与 ML 无关的项目,像是 Crhis Lattner 他们在做的 CIRCT 以及 MLIR in-tree 的 PDL。MLIR !=end-to-end ML 编译器。我觉可能是涉及 MLIR 的最大迷思吧。很多人看 MLIR 都是从 end-to-end ML 编译器的角度来看,就会觉得 MLIR 很奇怪,没有与 ML framework 的结合,没有完整的链路。但这些真的不是 MLIR core 想要解决的问题,也不是 MLIR core 需要提供的模块。
- 换言之,MLIR core 代码库里面其实没有必要存在任何的 dialect。MLIR core 对 out-of-tree dialect 的支持是其非常重要的设计根本,现在也比较完善。那 dialect 在MLIR core 里面存在的意义是什么呢?我个人认为有几点:1)提供复用的模块,2)让协作更容易,3)以及驱动 MLIR core 本身的演进。3)应该比较好理解。2)主要是工程考虑。在同一个代码库里面,特别是属于 LLVM project,很多大公司都不需要任何附加法律审核。协同效率会极大提高。1)其实比较有意思。其实可以做一个类比。MLIR core 相当于编译器的 C++。那 MLIR 代码库里面的 dialect 就是 STL。能够提供一套高效的共用库是语言成功的重要因素。(从这个角度考虑,end-to-end 编译器相当于用 C++ 和 STL 写成的具体项目。)从这个角度来考虑,能在 MLIR core 里面存在的 dialect 也是要过一个很高的标准的。MLIR 的正确食用方式是用其提供的基础工具和共用模块,再加上自己的逻辑穿针引线,来实现一个 end-to-end 编译器。MLIR 本身真的不能提供那个,也提供不过来。(Domain-specific 编译器可以有很多很多。)
- MLIR 生态尚处于早期,或者说很早期。MLIR 加入 LLVM project 也就才一年多一点。一个生态没有三五年真的很难完善。(作为对比,LLVM project 存在了快二十年了,TVM也快五年了吧。)很多时候很多问题像是为什么 MLIR 没有提供功能 A/B/C,回答很简单:还没有人有需求或者来得及实现而已。很多地方看起来比较凌乱,各种不完善,也只是项目发展的现状,而非最终状态。
- 我个人觉得 MLIR 最终想要建立一个有着各种比较独立的亚生态的生态圈。比如 CIRCT 可以形成自己的生态。我也可以用 MLIR 做 graphics 编译器,形成自己的生态。当然 LLVM 也有自己的亚生态,像是 Clang,像是 CodeGen。但这里是有区别的。CIRCT 与 基于 MLIR 的 graphics 编译器完全没有交集,而 Clang 和 CodeGen 是同一链条上的不同部分。生态圈的意义是,有许多公司许多人在用。软件开发离不开人,涉及人就离不开社交。如何平衡这么多人这么多需求来搭建一些共用的模块,怎么演进各个部分,这些在一定意义上甚至比单纯的技术更加复杂。从这种意义上说,MLIR 更是一种编译器软件开发的社交实验。(LLVM 或者其他大型的项目当然也有这种实践,但 MLIR 还是不同的。LLVM 还是强耦合的,如果有修改不提交给上游,那后面会很痛苦。但 MLIR 从本质上就讲求分散的。所有的 dialect 都可以在私有代码库里面,MLIR core 的变动引发的修改是比较低频和少量的。与上游交流的强驱动估计就是这些共用的 dialect 了...)
好了,啰嗦了这么多,希望能给大家理解 MLIR 带来一些思考。现在说回 Linalg dialect。
了解 Linalg dialect 首先需要了解一下现在的基于 MLIR 的编译器的整体架构。(当然,这不是唯一的架构,像是杨军就在他的回答里面指出他们有自己的想法。这里说的是贴近 IREE 演进方向的架构,也是我个人比较熟悉的。)ML 编译器的任务是把开发者写的高层次的 model 转化成贴合底层硬件架构的指令。这里对成熟的 CPU/GPU 和正在飞速发展的 domain-specific acclerator 要分开来看。对 CPU/GPU,基本就是产生各种嵌套的 loop 和 tile,针对 CPU/GPU 的不同层次的 compute/memory hierarchy。如果我们把整个栈从上到下划分一下,大体上就是前端高层次算子,中层 loop,下层 control flow,vector 和 scalar。MLIR 的 progressive lowering 目的就是在各个层级创建合适的 abstraction 来解决现在很多 ML framework 里面一步到位的问题。(新颖与否,是不是旧瓶装新酒,是不是有别的框架已经这么做了,我觉得都不是关键问题。大家相互借鉴是很正常的。工程上的推陈出新也是很重要的。)Linalg dialect 基本就处于高于中层 loop 的位置。这里的 surface area 非常大,可以探讨的设计可能性非常多。传统的 loop 优化已经有很多的很好的既有经验了,大家可以参见像是《Optimizing Compilers for Modern Architectures》等书。Linalg dialect 想借鉴很多既有想法(在题主的链接里面列了很多),来进行新的尝试。
我觉得 Linalg dialect 的核心是 transformation 优先。op 的定义是为了 transformation 来服务的。(注意这里有必要区别一下算子和 op。在 MLIR 生态里面所有的层级都可以定义 op。但底层的 op 显然是和现在的常见 ML framework 里面的算子有很大区别的。在这里我还是用 op 来表示 MLIR 里面的 op。厘清概念对理解还是很必要的。 )
Linalg 里面真正核心的 op 其实就是 linalg.generic 和 linalg.indexed_generic 两个。(后面统一称作 Linalg generic op。)这本身就让 transformation 非常容易写,因为基本只需要考虑这两个 op。Linalg generic op 本质是多层完美嵌套循环(perfect loop nest)的 op 化表示。Linalg generic op 里面用 indexing map 来隐性表示每层循环与输入输出的 access 关系,用附加的 region 表示针对这些输入输出进行的计算。这种设计从 IR 构建上就解决了很多传统 loop 优化的问题。因为根据定义,Linalg generic op 就是完美嵌套循环。针对 loop 做各种 transformation 的时候不可能存在非完美的情况,这样可以取消用来检测和维持 loop 完美性的逻辑。这可以算是 transformation 优先的一点展现吧。Transformation 会变得更易写、易读、易维护。使用 indexing map 来隐性表示每层循环与输入输出的关系也是让 transformation 优先的一点展现。举个例子,传统 loop 优化中如果要 fuse 两个 perfectly nested loop,需要分析每层 loop 的 induction variable 的 lower/upper bound 和 step,这些 induction variable 在 loop nest 里面 access 的 element,非常复杂。用 Linalg generic ops,只需要对 indexing map 进行 affine 操作:`inverse(producerIndexingMap).compose(consumerIndexingMap)`。(具体不再展开,想了解细节可以参见 Linalg Fushion 的代码。)其他的 transformation,像是 interchange、tiling、distribution 等等,也变得很简单,就不再一一举例了。
除了只有两个 generic op,Linalg dialect 中还有一个比较重要的概念,named ops。named ops 基本就是 generic ops 上面提供的 sugar:每个 named op 都有明确的隐性的 indexing map 和 compute region,它们定义了一个 named op。named ops 是可以和 generic op 相互转换的。(代码非常简单,不过现在只实现了 named ops 到 generic ops 的转换。)Named ops 存在的作用是和上层对接变得简单。算子层到 Linalg 层可以直接产生这些 named ops。但是在 Linalg 以及以下的层次上,transformation 主要操作的是 generic ops。确切地说是 generic ops 背后的 op interface。这样,我们可以狂加 named ops,但是编译器 transformation 确不需要修改,因为这些 named ops 都有同样的 op interface,既有 transformation 可以直接操作。这也是 transformation 优先的一点体现。(当然也不是说 transformation 完全不能操作 named ops。如果有针对某一 named op 的优化,也完全可以 match 那个 named op 然后写 transformation。这就是 Linalg generic op 到 named op 转换的初衷:我们可以随时在两种形态中变化。)除此之外,named ops 也是 CodeGen 中利用现有手写 kernel 库的途径。
Linalg dialect 以及其各种 transformation 已经在 IREE 中使用了。IREE 很早就已经可以完整编译一些 vision model 和 language model了。所以上面所说并不是完全的纸上谈兵,而是得到一定验证。
当然,Linalg dialect 也远非完美,还有很多改进空间。比如怎么表示 imperfect loop nest(一个想法是在 linalg.generic 的 region 里面允许 linalg.generic),比如怎么在 indexing map 里面支持 affine symbool,比如现在都是在搭建基础的 mechanism 而没有 ML/search-based policy solution 等等。Linalg dialect 总体上非常的节制,不是必须的东西不会随意添加。这会限制其表示能力,但这正是编译器所喜欢的。越细粒度限制越多的 semantics 编译器越喜欢。如果有一个 op 没有任何限制,表示力是爆表,但编辑器没法对它做任何操作。Linalg dialect 也处于比较迅速发展的过程中,像是现在开始完善对 tensor 的直接支持,等等。可以预见将来一些限制会随着需求的到来逐渐放开,但有一些也许永远不会。
1、先熟悉一下深度学习和机器学习,教材就不推荐了,很多,一定要动手实践,CV/NLP跑几个小模型,了解一下深度学习模型的怎么回事,有什么样的算子
你说没有GPU,这个不是问题,用CPU也可以。
2、深度学习编译器主要用于两个场景,AI框架或者AI芯片的配套编译器,可以先了解一下AI框架和深度学习编译器的全景知识,比如,深度学习编译器与传统编译器的区别
针对神经网络的编译器和传统编译器的区别和联系是什么?AI框架分析3、熟悉并实践业界常用的开源AI编译器,推荐TVM,先了解一下原理,然后看一下TVM中不同类型算子的实现,比如element-wise类、reduce类、matmul类、conv类等,最后自己可以实现几个简单的,把端到端的流程和原理摸清楚,包括compute、schedule、codegen等等。
TVM Documentation4、如果是做后端的AI编译器,需要了解一些硬件的编程知识,如GPU和NPU,GPU这一块有条件的话,推荐学习和实践一下cuda编程,NPU可以参考一下华为的昇腾
写CUDA到底难在哪?昇腾CANN系列教程-TBE算子开发(初级)_基础课程_华为云学院_云计算培训-华为云5、最后,也是最重要的,试着参与业界的开源框架社区或者到相关的公司去实习,重点了解实际场景下AI编译器的情况以及技能要求,并具备参与特性开发的能力,可以关注一下MindSpore社区(也算是打个广告),原因是:
- AI编译器做的比较全,包括图编译器(前端的硬件无关的,比如自动微分/自动并行;后端的硬件相关的优化)、算子编译器、端侧推理相关的编译器等等。
- 有大量的社区活动可以参加,比如模型和算子众筹、bug fix、MSG活动等等。
- 目前正在找实习生
可以,很多MCU的编译结果函数调用优化后可能都用不到栈,直接使用寄存器传参
也就是所谓的_fastcall,但fastcall显然是有适用条件的,例如有的时候你需要对参数取地址,并不是所有的MCU的寄存器都有地址映射
返回值存在寄存器里在大多数C编译器都适用,但如果是返回结构体的话,一般情况下并不会存储在寄存器里,这涉及到结构体成员寻址问题,你把所有成员变量都分布在不同寄存器里以后如何寻址,但如果非要做,也不是不能做,靠后期编译优化,部分适用函数也是能做到这种优化的,无非是做编译优化的多加加班.
但为什么MCU/IC出厂配套对应C编译链已经是业内共识,为什么不选C++/rust/go...之类的?究其根本:
1.最重要的C 编译工具链实现起来较为简单,如果你看不明白一件事,你就往这玩意能不能赚钱或者省钱上看.
2.拓展性强,你可以很容易捏一个编译特性(编译器拓展)以适配自己的IC(这是一把双刃剑,特殊的编译拓展会牺牲代码移植性,但完全统一的编译标准,注定只能适配部分的底层环境)
3.C作为老牌语言,已经在长远的时间内证明了其在工业界的稳定性与成熟性,学习相对简单,容易被大多数人接受.
最后一个拓展问题:C编译器是否可以在某些情况下不遵守调用约定(甚至是不遵守C语言标准)?
答:有没有想过,在底层环境中所谓的C语言,也许只是一个长得很像C语言的语言.
小贴士:Compiler engineer都是很傲娇的,如果你给ta一套编译标准,ta会表示"你说标准就标准,那我不是很没面子!".

作者|Chip Huyen
翻译|胡燕君、贾川、程浩源
我承认,在大学的编译器课上哭了,后来我选择成为一名机器学习工程师,以为再也不用被编译器烦扰。
然而,当我逐渐了解ML模型如何投入生产应用,关于编译器的问题不断涌现。在许多用例中,尤其是用边缘设备运行ML模型时,模型的成功与否仍然取决于运行它的硬件(https://hardwarelottery.github.io/)。因此,了解模型的编译和优化,以及模型在不同硬件加速器上的运行非常重要。
理想情况下,我们不需要特别关注编译器,一切都会“正常工作”。然而,要实现这个目标还有很长的路要走。
如今,越来越多公司希望用边缘设备运行ML模型,运行ML模型的硬件越来越多,为了让ML模型能在硬件加速器上更好地运行,也诞生了越来越多编译器——例如MLIR dialects、TVM、XLA、 PyTorch Glow、cuDNN等。根据PyTorch创始人Soumith Chintala的说法,随着ML的应用逐渐成熟,公司之间的竞争将转向谁能更好地编译和优化模型。

了解编译器的工作原理可以帮你选对编译器,让模型在所选硬件上的运行效果达到最佳,也能帮你诊断模型性能问题并加快模型运行速度。
本文对ML编译器进行了通俗介绍。ML编译器始于边缘计算的兴起,这使编译器不再是系统工程师的专属,而是全体ML从业者关心的领域。如果你已十分了解用边缘设备运行ML的重要性,可以跳过下文第一部分。
然后我将谈及在边缘设备部署ML模型的两个主要问题:兼容性和性能,并说明编译器如何解决这些问题,以及它的工作原理。本文最后还将提供关于如何通过几行代码来显著提高ML模型速度的参考资料。
想象一下,你已经训练出一个出色的ML模型,其精度远超你的期望,然后你迫不及待地部署这个模型,来让用户使用。
最简单的方法是将模型打包并通过托管云服务(如AWS或GCP)进行部署,这也是许多公司在最初使用ML时的做法。云服务在这方面贡献巨大,使得企业可以轻松将ML模型投入生产。
但是,云部署也有很多缺点。首先是成本。ML模型需要进行大量计算,而计算的成本很高。早在2018年,Pinterest、Infor、Intuit等大公司每年在云服务上的开销就已超数亿美元。而对于中小型公司来说,这个数字每年可能在5-200万美元之间。初创公司在云服务方面稍有不慎,可能就会导致破产。
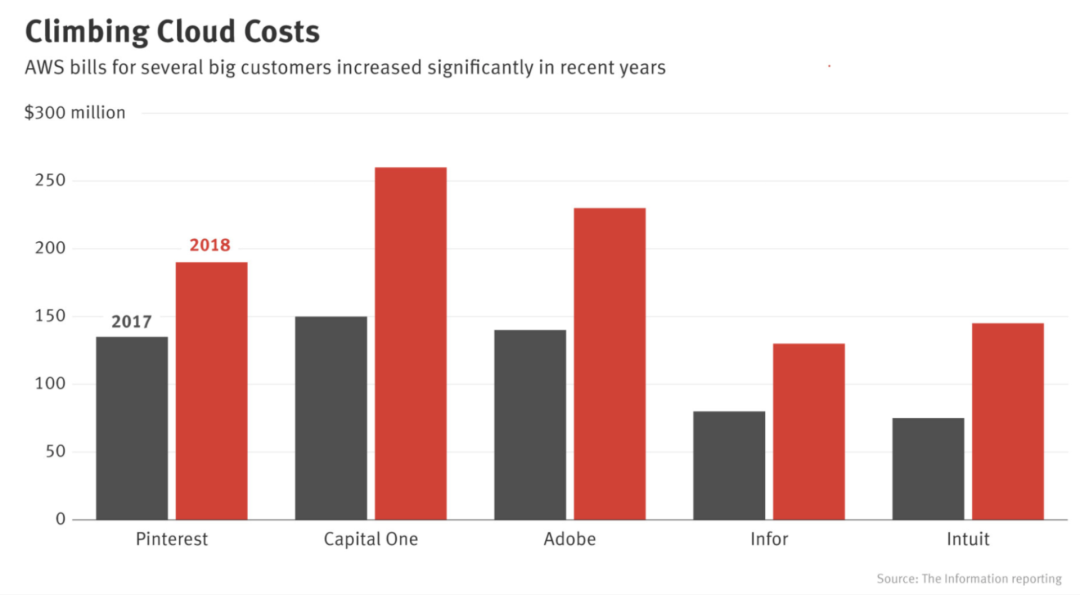
随着云计算费用不断攀升,越来越多公司试图将计算转移到消费设备(边缘设备)。在边缘设备上完成的计算越多,对云服务的需求就越少,他们要支付的费用就越少。
除了能降低成本,边缘计算还有许多优势。首先,边缘计算的可运行范围更广。当模型位于公有云上时,向云端发送并接收数据需要依赖稳定的网络连接。但边缘计算可以使模型在没有网络连接或连接不稳定的情况下继续运行,比如在农村地区或发展中国家。
其次,边缘计算可以减少网络延迟的困扰。如果必须使用网络传输数据(将数据发送到云端的模型进行预测,然后将预测发送回用户),那么某些用例可能就无法实现。在许多情况下,网络延迟比推理延迟更严重。例如,你或许能够将ResNet50模型的推理延迟从30毫秒降低到20毫秒,但其网络延迟可能会高达数秒,具体情况取决于你的所在地网络。
第三,边缘计算可以更好地保护敏感的用户数据。云计算ML模型意味着可能要通过网络来发送用户数据,增加了数据被拦截的风险。同时,云计算还将诸多用户的数据存储在同一位置,这意味着一旦发生数据泄露就会影响许多人。据《安全》杂志2020年报道,近80%的公司在过去18个月内曾遭遇过云数据泄露(https://www.securitymagazine.com/articles/92533-nearly-80-of-companies-experienced-a-cloud-data-breach-in-past-18-months)。边缘计算使得企业可以更安全地传输和存储用户数据,避免违反GDPR等数据保护条例。
相对于云计算,边缘计算具有许多优势,因此许多企业正竞相开发针对不同ML用例优化的边缘设备。谷歌、苹果、特斯拉等知名巨头都宣布自研芯片。与此同时,不少ML硬件初创公司也融资数十亿美元来开发更好的AI芯片。
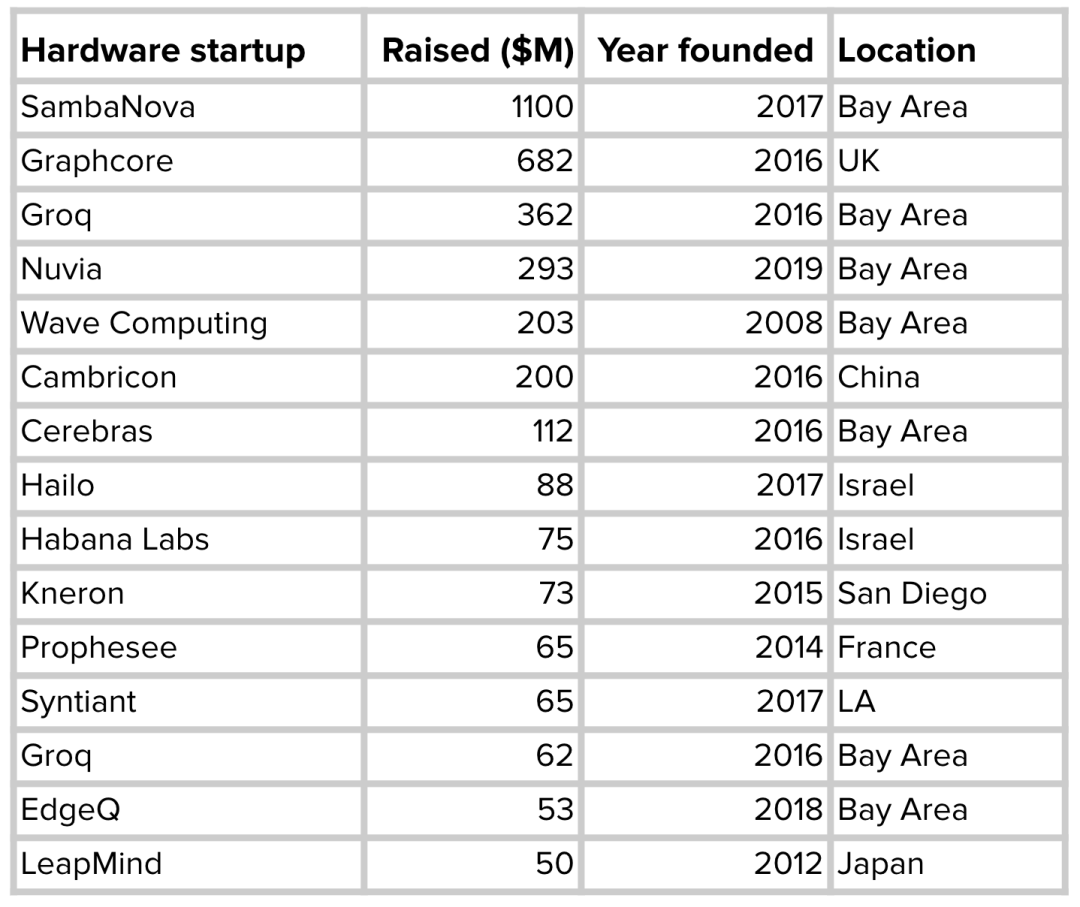
运行ML模型的硬件产品变多了,于是就出现一个问题:如何让使用任意框架构建的模型可以在任意硬件上运行?
一个框架要在某种硬件上运行,它必须得到硬件商的支持。例如,尽管Google早在2018年2月就已公开发布TPU,但直到2020年9月,TPU才支持PyTorch。在此之前,如果想使用TPU,就必须要使用Google的TensorFlow或JAX。
要使一种硬件(或平台)支持某一框架需要耗费大量时间和工作量。将ML工作负载映射到硬件需要了解并利用硬件的基础架构。然而,有一个基础性问题必须克服:不同的硬件类型有不同的内存布局和计算原语,如下图所示:
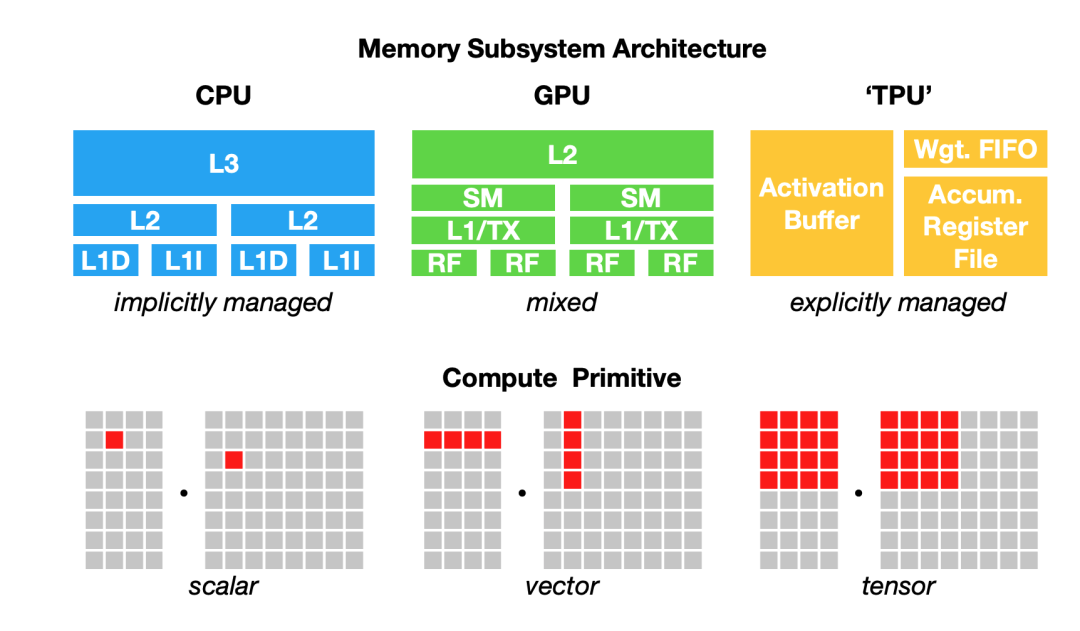
例如,从前,CPU的计算原语是数字(标量),GPU的计算原语是一维向量,而TPU的计算原语是二维向量(张量)。但是,如今许多CPU具有向量指令,而一些GPU具有二维张量核心。给定一个256张图像 x 3 通道 x 224 W x 224 H的batch,如果要对这个batch执行卷积算子,一维向量计算原语和二维向量计算原语将有很大不同。同样,还要考虑不同的L1、L2和L3布局和缓冲区大小,如此方能有效地利用内存。
正因如此,框架开发人员更倾向于只支持少数服务器级别的硬件(如GPU),而硬件商也倾向于只向少数框架提供自己的内核库(例如,英特尔的OpenVino工具库仅支持Caffe、TensorFlow、MXNet、Kaldi和ONNX。NVIDIA自己则有CUDA和cuDNN)。将ML模型部署到新硬件(例如手机、嵌入式设备、FPGA 和 ASIC)需要耗费大量的人力。

中间表示 (IR)
与其针对每种新的硬件类型和设备配备新的编译器和库,何不创建一个中间媒介来桥接框架和平台?框架开发人员将不再需要支持每种类型的硬件,而是只需将他们的框架代码“翻译”成这种中间媒介。这样,硬件商就只需要支持一个中间框架。
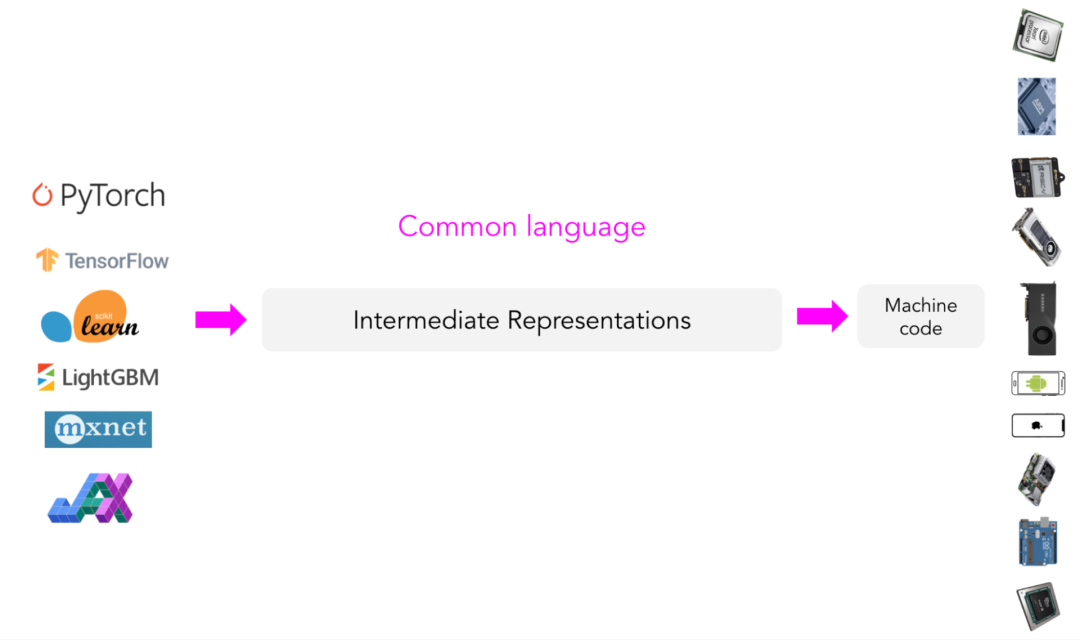
这种中间媒介称为中间表示(IR)。IR是编译器工作的核心。编译器在模型原始代码的基础上生成一系列高级和低级中间表示,然后生成硬件原生代码以在特定平台上运行模型。
编译器通常利用代码生成器(codegen)根据IR生成机器原生代码。ML编译器中最常用的代码生成器是Vikram Adve和Chris Lattner开发的LLVM,LLVM改变了我们对系统工程的理解。TensorFlow XLA(译注:2022年10月,Google宣布开源OpenXLA)、NVIDIA CUDA编译器 (NVCC)、MLIR(用于构建其他编译器的元编译器)和TVM都在使用LLVM。
生成代码的过程也称为“降级(lowering)”,因为是将高级的框架代码“降低”为低级的硬件原生代码。准确地说,这个过程不能称作“翻译”,因为两种代码之间不是一对一的映射关系。
高级IR通常是ML模型的计算图。对于熟悉TensorFlow的人来说,这里的计算图类似TensorFlow 1.0中的计算图,那时TensorFlow还没有切换到Eager Execution模式。TensorFlow 1.0在运行模型之前会先构建模型计算图,计算图可让TensorFlow了解模型,从而优化运行时。
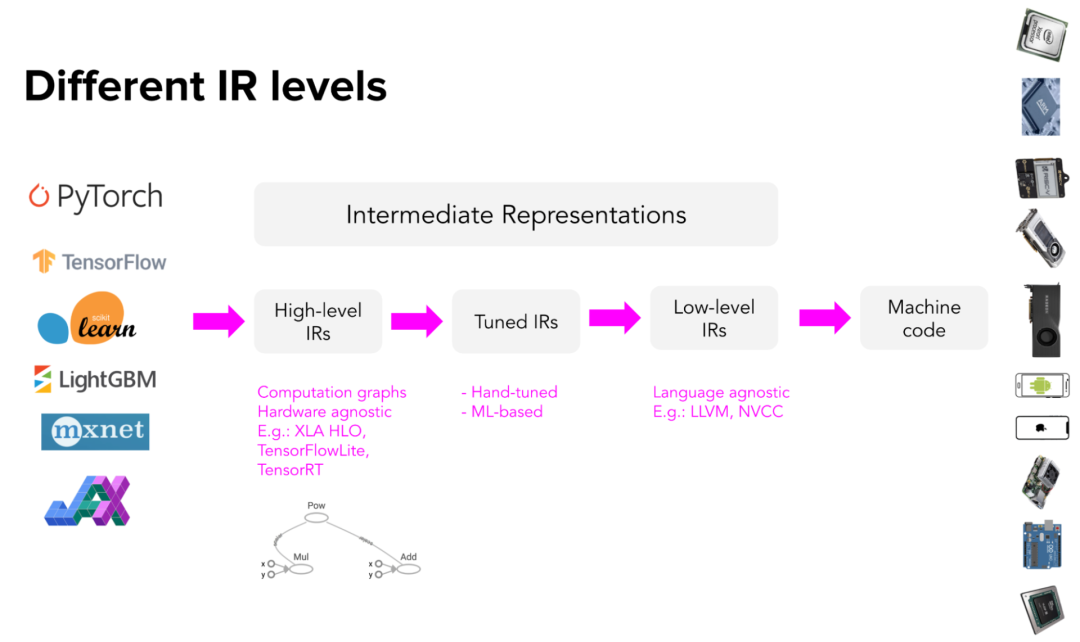
高级IR通常与硬件无关(无论在什么硬件上运行),而低级IR通常与框架无关(无论模型是用什么框架构建的)。
完成代码“降级”后,在所选硬件上运行模型时可能还会遇到性能问题。Codegen非常擅长将IR降级为机器代码,但受目标硬件后端的影响,机器代码的运行效果可能不够好。生成的代码可能无法充分利用数据局部性和硬件缓存,或者无法使用可以加速代码的高级功能,例如向量操作或并行操作。
典型的ML工作流程需要用到许多框架和库。例如,用 Pandas/Dask/Ray 从数据中提取特征;用NumPy执行向量化;用LightGBM等树模型来生成特征,然后用由不同框架(如sklearn、TensorFlow或Transformers)构建的各种模型来进行预测。
尽管这些框架内部的个别功能可能得到优化,但跨框架的优化几乎不存在。一种简单的方法是把数据搬运到不同的功能上分别计算,但这会导致整个工作流的速度下降一个数量级。斯坦福 DAWN实验室的研究人员的一项研究发现:与手动优化代码相比,使用NumPy、Pandas和TensorFlow的典型ML工作负载在一个线程中的运行速度要慢23倍(http://www.vldb.org/pvldb/vol11/p1002-palkar.pdf)。
在生产中,数据科学家/ML工程师常用pip来安装他们工作所需的包,在开发环境中运行状况良好,于是他们将模型部署到生产环境。当他们在生产中遇到性能问题时,他们的所在公司通常会聘请优化工程师来根据运行的硬件优化模型。


然而优化工程师十分稀缺,薪资要求也高,因为这份工作既要懂机器学习,也要懂硬件架构。另一个办法是采用优化编译器(Optimizing Compiler),即可以优化代码的编译器,也可以自动优化模型。在将ML模型代码降级为机器代码的过程中,编译器可以分析模型计算图以及其中包含的算子(如卷积算子、循环算子、交叉熵等),然后设法加快计算速度。
前文总结:编译器可以把ML模型和它赖以运行的硬件桥接起来。优化编译器包含两部分:降级与优化。这两部分有时也可以整合在一起。优化可能发生在从高级IR到低级IR的任何阶段。
- 降级:编译器为模型生成硬件原生代码,让模型可以在特定硬件上运行。
- 优化:编译器根据硬件环境优化模型。
优化ML模型的方法有两种:局部优化和全局优化。局部优化是指优化模型的某一个或某一组算子;全局优化是指端到端优化整个计算图。
目前已有一些标准的局部优化方法,大部分是通过提高并行度或减少芯片内存访问来加速模型。以下是四种常见的方法。
- 向量化:给定一个循环或嵌套循环,但单次不止执行一个元素,而是使用硬件原语执行在内存中连续的多个元素。
- 并行:给定一个输入数组(或者n维数组),将其分割为多个不同的独立工作块,分别对每个工作块执行操作。
- 循环分块(Loop Tiling):修改循环中的数据访问顺序,从而更好地利用硬件的内存布局和缓存。这种优化方法对硬件的依赖极高。适合CPU的访问模式未必适合GPU。详情可参考Colfax Research提供的可视化解释
(https://colfaxresearch.com/how-series/#ses-10)。 - 算子融合:将多个算子融合为一个算子,可以避免冗余的内存访问。例如,对同一数组执行两个操作需要两次循环,但经过融合后就只需要一次循环。详情可参考Matthias Boehm提供的例子。(https://mboehm7.github.io/teaching/ss19_amls/04_AdvancedCompilation.pdf)


Weld编译优化器的缔造者Shoumik Palkar表示,在一定的条件下,这些标准局部优化方法可以将模型运行速度提升3倍左右。(https://www.youtube.com/watch?v=JbTqNuCIJM4)
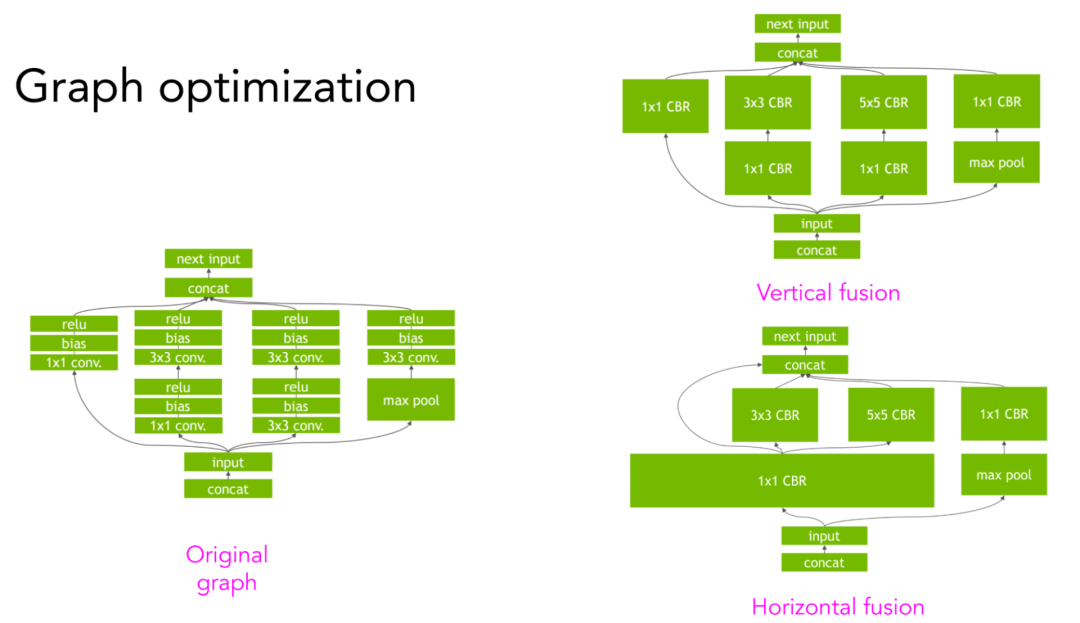
实现更大的速度提升需要运用到计算图中更高层次的结构。例如,给定一个卷积神经网络及其计算图,可进行垂直或水平方向的融合,从而减少内存访问,加快模型运行速度。详情可参考NVIDIA的TensorRT 团队提供的可视化解释(https://developer.nvidia.com/tensorrt)。
人工设计优化规则
正如上文的垂直/水平融合例子所示,执行计算图的方法很多。例如,给定3个算子A、B、C,可以融合A与B,B与C,也可融合A、B、C。
通常,框架和硬件商的优化工程师能根据经验探索出执行模型计算图的最佳方法。例如,NVIDIA可能会安排一名工程师甚至一个工程师团队来专门研究如何让ResNet-50模型在NVIDIA的DGX A100服务器上运行得更快(所以,不应太看重MLPerf基准测试结果(https://mlcommons.org/en/inference-datacenter-10/)。因为即使一种常见模型在某种硬件上可以运行得相当快,也并不代表任何模型使用该种硬件都能获得同样的高速度。这种模型可能只是经过过度优化而已)。
人工设计优化规则有一些不足之处。首先,得出的优化规则可能不是最优的。谁也不能保证工程师想出来的优化方法就是最佳方案。
其次,人工设计出的优化规则不具备自适应性。如果要针对新的框架或新的硬件架构优化模型,还得重新耗费大量人力。
何况,模型优化取决于计算图中的算子,这又增加了复杂性。优化卷积神经网络不同于优化递归神经网络,后者又不同于优化Transformer模型。NVIDIA和Google专注于针对自家硬件优化ResNet和BERT等常见模型。但如果ML研究人员又发明出新的模型架构呢?那他们就得先自行优化这种新模型,证明它具备高性能,才能让硬件商采用并继续优化这种模型。
用ML来加速ML模型
我们的目标是找到执行计算图的最快方法。那么能不能将所有可能的方法都尝试一遍,记录每种方法的运行时间,然后找到时间最短的一种呢?
可以。但问题是,潜在的方法及其组合实在太多,难以一一穷尽。但如果借助ML呢?
- 用ML可以缩小搜索空间(即所有可能方法的集合),不必尝试所有方法。
- 用ML还可以预测每种方法的所需用时,不必耗费时间等待计算图完成执行。
然而,要预估某种方法执行计算图的所需用时非常困难,因为这需要对计算图作出大量假设。目前的技术只能做到关注计算图的一小部分。
如果你曾在GPU上运行PyTorch,你应该见过下列设置:
torch.backends.cudnn.benchmark=True当设置为True时,就启用了cuDNN autotune。cuDNN autotune会在一组预先设定的执行卷积算子的方法中探索最快的一种。如果每次迭代的卷积神经网络形状都一致,启用cuDNN autotune可以大大提高效率。除了首次运行卷积算子时速度较慢以外(因为cuDNN autotune需要花时间探索最快的方法),在后续运行中,cuDNN都可以利用autotune的缓存结果直接选择最快的配置。
虽然cuDNN autotune可以提高效率,但它只适用于卷积算子,而且应该只在PyTorch和MXNet上能用。更通用的解决方案是autoTVM,它是开源编译器堆栈TVM的一部分。autoTVM可针对子图寻找最佳执行方法,而不只是针对一个算子,所以它的搜索空间要复杂得多。autoTVM的工作原理也很复杂,但可以总结如下:
1. 将计算图分割为多个子图。
2. 预测每个子图的大小。
3. 分配时间为每个子图寻找最佳执行方法。
4. 将每个子图的最佳执行方法组合起来,执行整个计算图。
autoTVM能计算每种方法的实际运行时间,从而收集真实数据用以训练成本模型,令成本模型预测未来某种方法的所需时间。这种做法的好处是,由于成本模型是根据运行时产生的数据训练的,所以它可以适应任何硬件,坏处是等待成本模型训练完善需要更长时间。
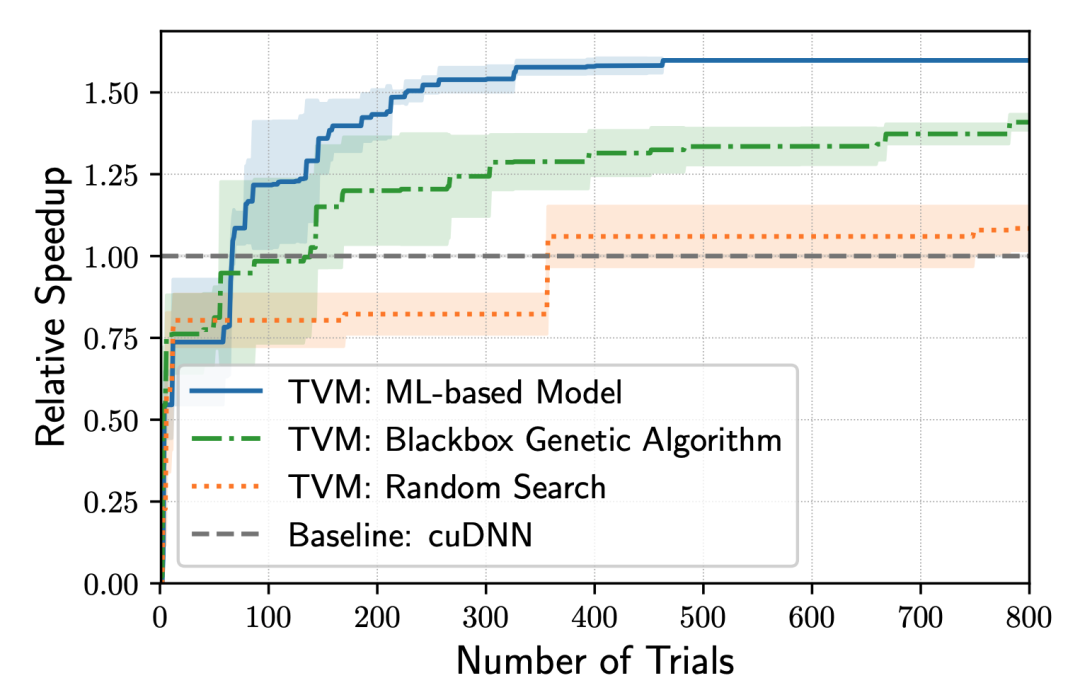
TVM之类的编译器具有自适应性、灵活性,能帮助用户方便地尝试新硬件,例如苹果公司在2020年11月发布的M1芯片。
M1是一个基于ARM的片上系统(SoC),ARM架构我们或多或少都有所了解,但是M1的ARM实现仍然有很多新颖的地方,需要大量优化才能使各种ML模型在M1芯片上快速运行。
在M1芯片发布一个月后,OctoML(译注:TVM团队2019年成立的公司,专注于ML模型的部署)表示,autoTVM 进行的优化比苹果公司的Core ML团队人工设计的优化快了近 30%(https://venturebeat.com/2020/12/16/octoml-optimizes-apache-tvm-for-apples-m1-beats-core-ml-4-by-29/)。当然,随着M1的成熟和人工优化的深入发展,自动优化将很难超越人工优化,但系统工程师仍可以利用autoTVM等自动优化工具来加速优化。
虽然自动优化的效果突出,但依然存在一个问题:TVM的速度有可能很慢。需要试遍所有的可能方法,才能确定最佳优化路径,这一过程可能需要耗费数小时,复杂的ML模型甚至可能需要数天。但这是一劳永逸的过程,优化搜索的结果可以被缓存,然后用于优化现有模型,还可以为未来的优化提供基础。
当你针对一种硬件后端优化了一次模型之后,该模型就可以在使用同一硬件后端的多种设备上运行。当你准备好用于生产的模型,并且选定目标硬件来运行推理时,这种优化方法非常适用。
目前最广泛使用的编译器类型,是由主流框架和硬件商开发的、针对特定框架和硬件组合的特定领域编译器。不出所料,最常用的编译器是由最大的框架和硬件商开发的。
- NVCC(NVIDIA CUDA编译器):闭源;仅适用于 CUDA。
- XLA(加速线性代数编译器,由Google开发):已作为TensorFlow库的一部分开源;XLA原本打算用于加速TensorFlow模型,但已被运用到JAX。
- PyTorch Glow(Facebook):已作为PyTorch库的一部分开源;虽然在TPU上启用了XLA+PyTorch,但对于其他硬件还是依赖PyTorch Glow。
第三方编译器通常雄心勃勃(如果某编译器开发商认为自己针对GPU进行的模型优化比NVIDIA做得还要好,这必然需要足够的自信)。第三方编译器的存在很重要,在知名巨头已针对自家产品深度调整自家编译器的情况下,第三方编译器可以帮助小公司推出的新框架、新硬件和新模型时降低开销、提高性能,让小公司也有机会与知名巨头竞争。
我心目中最好的第三方编译器是Apache TVM,它适用于多种框架(包括TensorFlow、MXNet、PyTorch、Keras、CNTK)和多种硬件后端(包括CPU、服务器GPU、ARM、x86、 移动GPU和基于FPGA的加速器)。
另一个我看好的项目是MLIR。它最初也是由LLVM的创建者Chris Lattner在Google发起,但现在,该项目隶属LLVM。MLIR并不是真正意义上的编译器,而是一种元编译器,一种可以让用户构建自己的编译器的基础架构。MLIR可以运行多种IR,包括TVM的IR、LLVM的IR和TensorFlow计算图。
WebAssembly (WASM)
WASM是过去几年中最令我兴奋的技术趋势之一。它拥有高性能、易于使用,而且它的生态发展飞快。截至2021年9月,全球93%的设备都支持WASM。
我们一直在讨论编译器如何为模型生成机器原生代码,让模型可以在特定的硬件后端上运行。那能不能生成一种可以在任何硬件后端上运行的代码?
浏览器有一个好处:如果你的模型可以在浏览器上运行,那么这个模型就可以在任何支持浏览器的设备上运行,包括Macbook、Chromebook、iPhone、Android手机等,且无需关心这些设备使用什么芯片。如果苹果决定从英特尔芯片改用ARM芯片,对你也没有影响。

WASM是一个开放标准,它让你得以在浏览器上运行可执行程序。使用sklearn、PyTorch、TensorFlow等框架构建模型后,你不必针对特定硬件编译模型,而是可以将模型编译为WASM。然后你会得到一个可执行文件,可以用JavaScript来执行该文件。
因为WASM是在浏览器中运行,所以它的缺点是速度很慢。尽管WASM已经比JavaScript快得多,但与在设备上运行原生代码相比(例如iOS或Android应用程序),它仍然很慢。Jangda等人的研究显示,编译为WASM的应用程序,其运行速度比原生应用程序平均慢45%(火狐浏览器)到55%(谷歌浏览器)(https://www.usenix.org/conference/atc19/presentation/jangda)。
有许多编译器可以将代码编译到WASM运行时。例如最流行的Emscripten(它使用的也是LLVM Codegen),但它只能将C语言和C++编译成WASM;Scailable可以将scikit-learn模型编译为WASM,但它在GitHub上只有十几个Star,并且已经有几个月没更新了(开发方是不是已经不再维护它了?);TVM应该是目前还能用的唯一一个可将ML模型编译到WASM的编译器(https://tvm.apache.org/2020/05/14/compiling-machine-learning-to-webassembly-and-webgpu)。
温馨提示:如果你打算使用TVM的话,用非官方conda/pip命令可以快速安装(https://tlcpack.ai/),不要看Apache站点上的说明。因为如果你按照后者操作遇到问题,只能去他们的Discord上找人帮忙(https://discord.gg/8jNs8MkayG)。
思考模型在不同的硬件后端上的运行细节很有必要,这样有助于提高模型性能。Austin Huang(https://www.linkedin.com/in/austin-huang-74a75422/)在MLOps Discord上发帖称,只需使用简单的现成工具,例如量化工具、Torchscript、ONNX、TVM等,往往就可以获得两倍的模型加速。
在此我向大家推荐一篇文章(https://efficientdl.com/faster-deep-learning-in-pytorch-a-guide/),它列出了多个在GPU上加速PyTorch模型的有用技巧,甚至无需使用编译器。
在模型部署阶段,有必要尝试不同的编译器,比较哪一个可以带来最佳的性能提升。你可以并行进行实验。如果一个推理请求获得小幅提速,那么数百万或数十亿推理请求就可以累积成巨大回报。
尽管用于机器学习的编译器已经取得巨大进步,但我们还需要很多努力,才能把编译器抽象出来,让广大ML从业者不用再为编译器烦恼。理想的情况是,ML编译器可以像GCC传统编译器一样。GCC会自动将C语言或C++代码降级为机器代码,让大多数C语言程序员不必关心GCC会生成什么中间表示。
未来,相信ML编译器也可以做到这样,当开发者使用框架创建出计算图形式的ML模型,然后ML编译器可以根据任何目标硬件为模型生成机器原生代码,开发者也不必关心编译器生成什么中间表示。TVM等工具可以帮助我们实现这一未来。
感谢Luke Metz、Chris Hoge、Denise Kutnick、Parimarjan Negi、Ben Schreiber、Tom Gall、Nikhil Thorat、Daniel Smilkov、Jason Knight和Luis Ceze,他们耐心地回答了我的问题,帮助我写出了这篇文章。
(本文经授权后由OneFlow编译发布,原文:https://huyenchip.com/2021/09/07/a-friendly-introduction-to-machine-learning-compilers-and-optimizers.html。译文转载请联系OneFlow获得授权。)
其他人都在看
- TVM:成为深度学习领域的“Linux”
- 进击的PyTorch,和它背后的开源领袖
- TPU演进十年:Google的十大经验教训
- LLVM之父Chris Lattner:编译器的黄金时代
- 开源吞噬AI界?从Stable Diffusion的爆火说起
- OneEmbedding:单卡训练TB级推荐模型不是梦
- 大模型训练难?效率超群、易用的“李白”模型库来了
欢迎体验OneFlow最新版本:
https://github.com/Oneflow-Inc/oneflow/虽然C++的二进制膨胀在某些场景下确实是个问题,但是在正常情况下也不可能编译出大小为700KiB的hello world二进制文件
下次请先展示environment
操作系统:wsl2 ubuntu 22.04
内核版本:5.15.79.1-microsoft-standard-WSL2
编译器:gcc 11
#include <iostream>
using namespace std;
int main() {
cout << "Hello world";
return 0;
}
随便开几个优化二进制大小的选项:
> g++ -Os -fno-stack-protector -fno-rtti -fno-exceptions -ffunction-sections -fdata-sections -Wl,--gc-sections a.cc
> ls -l https://www.zhihu.com/topic/a.out
16216就算什么都不开:
> g++ -O0 -g a.cc && ls -l https://www.zhihu.com/topic/a.out
32664在windows 10下使用mingw编译二进制最大也仅有60KiB
除了陈天奇老师的课,其实还有一个【AI编译器原理】的系统介绍。
随着深度学习的应用场景的不断泛化,深度学习计算任务也需要部署在不同的计算设备和硬件架构上;同时,实际部署或训练场景对性能往往也有着更为激进的要求,例如针对硬件特点定制计算代码。
这些需求在通用的AI框架中已经难已得到满足。由于深度学习计算任务在现有的AI框架中往往以DSL(Domain Specific Language)的方式进行编程和表达,这本身使得深度学习计算任务的优化和执行天然符合传统计算机语言的编译和优化过程。因此,【AI编译器】深度学习的编译与优化就是将当前的深度学习计算任务通过一层或多层中间表达进行翻译和优化,最终转化成目标硬件上的可执行代码的过程。本系列将围绕现有【AI编译器】中的编译和优化工作的内容展开介绍。
通过【AI编译器原理】这个系列内容,以及这门课程后面的几门课程,你将获取并且掌握的技能:
- 《传统编译器》会粗略地回顾传统编译器中的前端、后端、IR中间表达等主要的概念,并对目前主流的两大编译器GCC和LLVM进行简单的展开,去了解GCC的编译流程和编译方式,并回顾LLVM的整体架构。
- 《AI 编译器》是本节的概览重点,去了解本章的主要内容 AI 编译器的整体架构,包括他的发展阶段,目前主要的组成模块,整体的技术演进方向等概念性的内容,因为近年来AI编译器发展迅猛,可以横向去了解AI编译器整体技术。
- 《前端优化》前端优化作为 AI编译器 的整体架构主要模块,主要优化的对象是计算图,而计算图是通过AI框架产生的,值得注意的是并不是所有的AI框架都会生成计算图,有了计算图就可以结合深度学习的原理知识进行图的优化。
- 《后端优化》后端优化作为AI编译器跟硬件之间的相连接的模块,更多的是算子或者Kernel进行优化,而优化之前需要把计算图转换称为调度树等IR格式,然后针对每一个算子/Kernel进行循环优化、指令优化和内存优化等技术。
- 《多面体技术》多面体不属于新的技术,反而是传统编译器的一种优化手段,得益于深度学习中的主要特征(循环、张量),因此多面体技术可以发挥更大的作用,对循环展开、内存映射等优化工作。
- 《PyTorch图模式》会以实际的AI框架 PyTorch 2.0为主线,去把其主打特性 Dynamo 和 AOTAutograd 进行展开,并回顾 PyTorch 对图模式的尝试,了解现今最热门的AI框架如何进行编译器优化的。
希望这个系列能够给大家、朋友们带来一些些帮助,也希望自己能够继续坚持完成所有内容哈!
然这里不是打广告,而是希望跟所有关注开源项目的好朋友一起探讨研究,共同促进学习讨论,也欢迎各位专家和朋友多拍拍砖,多提点意见。相关的材料都开源在这里:https://github.com/chenzomi12/DeepLearningSystem/tree/main/Compiler

- 课程概述 video
- 开源编译器的发展 video
- GCC编译过程和原理 video
- LLVM设计架构 video
- (上) LLVM IR详解 video
- (中) LLVM前端和优化层 video
- (下) LLVM后端代码生成 video
- 内容介绍 video
- 计算图层IR video
- 算子融合策略 video
- (上) 布局转换原理 video
- (下) 布局转换算法 video
- 内存分配算法 video
- 常量折叠原理 video
- 公共表达式消除 video
- 死代码消除 video
- 代数简化原理 video
- PyTorch2.0 特性串讲 video
- TorchScript 静态图尝试 video
- Torch FX 与 LazyTensor 特性 video
- TorchDynamo 来啦 video
- AOTAutograd 原理 video
- Dispatch 机制 video
完结,撒花!
xinet:TVM编译之解析 TVM Graph JSON创建双头输出小网络:
import numpy as np
from tvm.relay.build_module import bind_params_by_name
x=relay.var("x", shape=(1, 1, 8, 8), dtype="int8")
w=relay.var("w", shape=(2, 1, 3, 3), dtype="int8")
conv2d=relay.op.nn.conv2d(x, w)
relu=relay.op.nn.relu(conv2d)
mod=tvm.IRModule.from_expr(relay.Tuple([conv2d, relu]))
mod["main"]=bind_params_by_name(mod["main"],
{"w": tvm.nd.array(np.ones(shape=(2, 1, 3, 3),
dtype="int8"))})
rt_lib=relay.build(mod, target="llvm")
rt_lib.params.keys(), rt_lib.params["p0"].shape, rt_lib.params["p0"].dtype结果:
(dict_keys(['p0']), (2, 1, 3, 3), 'int8')此网络结构如下:
print(rt_lib.ir_mod)
显示
def @main(%x: Tensor[(1, 1, 8, 8), int8]){
%0=nn.conv2d(%x, meta[relay.Constant][0], padding=[0, 0, 0, 0]);
%1=nn.relu(%0);
(%0, %1)
}查看 Graph Json:
bunch=eval(rt_lib.graph_json)
print(toml.dumps(bunch))bunch结果:
arg_nodes=[ 0, 1,]
heads=[[ 2, 0, 0,],[ 3, 0, 0,],]
node_row_ptr=[ 0, 1, 2, 3, 4,]
[[nodes]]
op="null"
name="x"
inputs=[]
[[nodes]]
op="null"
name="p0"
inputs=[]
[[nodes]]
op="tvm_op"
name="tvmgen_default_fused_nn_conv2d"
inputs=[[ 0, 0, 0,],[ 1, 0, 0,],]
[nodes.attrs]
num_outputs="1"
num_inputs="2"
flatten_data="0"
func_name="tvmgen_default_fused_nn_conv2d"
out_layout=""
kernel_layout="OIHW"
data_layout="NCHW"
hash="8f5bab575bcb83dc"
[[nodes]]
op="tvm_op"
name="tvmgen_default_fused_nn_relu"
inputs=[[ 2, 0, 0,],]
[nodes.attrs]
num_outputs="1"
num_inputs="1"
flatten_data="0"
func_name="tvmgen_default_fused_nn_relu"
hash="fd6e720bc47ba75c"
[attrs]
dltype=[ "list_str",[ "int8", "int8", "int8", "int8",],]
device_index=[ "list_int",[ 1, 1, 1, 1,],]
storage_id=[ "list_int",[ 0, 1, 2, 3,],]
shape=[ "list_shape",[[ 1, 1, 8, 8,],[ 2, 1, 3, 3,],[ 1, 2, 6, 6,],[ 1, 2, 6, 6,],],]定义计算图节点类型枚举类:
/*! \\brief Node types */
enum GraphNodeType {
kGraphNop,
kGraphInputNode,
kGraphOpNode,
};
使用 Python 实现为:
from enum import Enum
class GraphNodeType(Enum):
"""节点枚举类型
Attrs:
kGraphNop: 非算子节点
kGraphInputNode: 参数节点的索引列表,它是计算图的占位符/变量/输入节点 或 constant/param。
kGraphOpNode: 算子节点
"""
kGraphNop: int = 0
kGraphInputNode: int = 1
kGraphOpNode: int = 2节点基类定义如下:
/*! \\brief Base Node class */
class GraphNode {
public:
GraphNode() {}
virtual void Save(dmlc::JSONWriter* writer) const {}
virtual void Load(dmlc::JSONReader* reader) {}
virtual GraphNodeType Type() const { return kGraphNop; }
virtual ~GraphNode() {}
public:
int num_outputs_{1};
std::string name_;
GraphAttrs attrs_;
};
使用 Python 实现:
from typing import Any
from dataclasses import dataclass
from abc import ABC, abstractmethod
GraphAttrs = dict[str, Any]
@dataclass
class GraphNode(ABC):
name: str
attrs: GraphAttrs
num_outputs: int = 1
@abstractmethod
def Save(self, writer) -> None:
...
@abstractmethod
def Load(self, reader) -> None:
...
@abstractmethod
def Type(self) -> GraphNodeType:
return GraphNodeType.kGraphNop输入节点:
/*! \\brief Input Node */
class GraphInputNode : public GraphNode {
public:
GraphInputNode() {}
GraphInputNode(const std::string& name, const GraphAttrs& attrs) {
name_ = name;
attrs_ = attrs;
}
GraphNodeType Type() const override { return kGraphInputNode; }
void Save(dmlc::JSONWriter* writer) const override {
const std::string op_name{"null"};
writer->BeginObject();
writer->WriteObjectKeyValue("op", op_name);
writer->WriteObjectKeyValue("name", this->name_);
writer->WriteObjectKeyValue("inputs", std::list<int>());
writer->EndObject();
}
static std::shared_ptr<GraphNode> make_node_ptr(const std::string& name,
const GraphAttrs& attrs) {
auto ptr = std::make_shared<GraphInputNode>(name, attrs);
return std::dynamic_pointer_cast<GraphNode>(ptr);
}
};
使用 Python 实现
@dataclass
class GraphInputNode(GraphNode):
inputs: list[int] = []
def Type(self) -> GraphNodeType:
return GraphNodeType.kGraphInputNode
def Save(self, writer) -> None:
bunch = {
"op": "null",
"name": self.name,
"inputs": self.inputs
}
# 写入到 writer 句柄
...
def Load(self, reader) -> None:
...
def make_node_ptr(self):
# make_node(name, attrs)
...
同样使用 Python 实现算子节点类:
@dataclass
class GraphNodeRef:
ident: int # 节点引用索引
index: int = 0 # 暂不知作用
version: int = 0 # 暂不知作用
@dataclass
class GraphOpNode(GraphNode):
nd_attrs: GraphAttrs
op_name: str
inputs: list[GraphNodeRef]
num_outputs: int = 1
def __post_init__(self):
self.attrs["func_name"] = self.op_name
self.attrs["flatten_data"] = "0"
self.attrs["num_inputs"] = str(sum(self.inputs))
self.attrs["num_outputs"] = str(self.num_outputs)
def Type(self) -> GraphNodeType:
return GraphNodeType.kGraphOpNode
def Save(self, writer) -> None:
bunch = {
"op": "tvm_op",
"name": self.name,
"attrs": self.attrs,
"inputs": self.inputs
}
# 写入到 writer 句柄
...
def Load(self, reader) -> None:
...
def make_node_ptr(self):
# make_node(name, nd_attrs, op_name, inputs, attrs, num_outputs)
...代码生成器 GraphExecutorCodegen图执行器的代码生成器,生成包含 Graph JSON、模块和模块的参数。
@dataclass
class LoweredOutput:
graph_json: str
lowered_funcs: dict[str, tvm.IRModule]
external_mods: list[tvm.IRModule]
params: dict[str, tvm.runtime.NDArray]
@dataclass
class GraphExecutorCodegen:
mod: tvm.runtime.Module
targets: list[tvm.target.Target]
def GetStorageInfo(self, expr) -> "tvm.relay.backend.StorageInfo":
"""获取单个表达式的存储信息"""
...
def Codegen(self, mod: tvm.IRModule,
func: relay.Function,
mod_name: str) -> "tvm.relay.backend.LoweredOutput":
"""
1. lowering 前需要规划内存并更新 workspace 大小
2. 获取 lowered_main_func
3. 将所有参数转换为输入节点。
4. 收集外部代码生成的任何运行时模块。
5. 收集外部代码提取的任何常量。
6. 收集在 lowering 过程中提取的任何常数。
7. 按目标分隔模块中的函数
8. 需要保存 Graph Json 到输出
"""
...我之前维护了一个仓库
https://github.com/BBuf/tvm_mlir_learn用来记录mlsys相关的学习博客或者视频,主要是 llvm/tvm/mlir 相关的,最近又整理并更新了一些资料。对于想入门mlsys或者想深入学习某种编译器的开发者来说,希望这个仓库可以成为不错的起点。下面的内容是这个仓库的README预览,欢迎star和分享。
更加重要的是,欢迎大家一起维护这个mlsys资料整理的仓库,让入门llvm/tvm/mlir的国内小伙伴可以找到一手并且集中的资源。直接提pr修改readme即可,或者联系我让我加一下资料链接。
持续更新中...
- What Is MLIR && What Is TVM?
- TVM Conf 2020 - An Introduction to TVM Part1
- TVM Conf 2020 - An Introduction to TVM Part2
- Torch MLIR公开会议翻译视频(自制中英双字完整版)
- TVM命令行驱动程序 视频教程
- 基于 MLIR 完成对 GEMM 的编译优化 中英视频上,中部分
- TVM TensorIR 视频讲解(熟肉)
- What Is LLVM?
- How To Install LLVM?
- Running the LLVM Tools
- LLVM IR介绍
LLVM 系列视频对应的源码在:https://github.com/lac-dcc/llvm-course
LLVM相关的视频比较少,youtube上比较多,上面 GiantPandaCV 翻译的几期 LLVM 入门视频也是来源于 youtube,大家可以自行查找学习。
- 人工智能编译器MLIR-官方入门教程讲解
- MLIR Toy Tutorial概述
- MLIR & python binding简介
- [MLIR]使用MLIR完成一个端到端的编译流程
- TPU-MLIR系列讲解(一):AI编译器是啥?
- TPU-MLIR系列讲解(二):TPU-MLIR简介
- TPU-MLIR系列讲解(三):MLIR语法介绍(上)
- TPU-MLIR系列讲解(四):MLIR语法介绍(中)
- TPU-MLIR系列讲解(五):MLIR语法介绍(下)
- TPU-MLIR系列讲解(六):前端转换
- TPU-MLIR系列讲解(七):MLIR- Dialect Conversion
- TPU-MLIR系列讲解(八):Lowering in TPU-MLIR
- TPU-MLIR系列讲解(九):量化概述
- TPU-MLIR系列讲解(十):量化推导
- TPU-MLIR系列讲解(十一):量化校准
- TPU-MLIR系列讲解(十二):量化感知训练
- TPU-MLIR系列讲解(十三):精度验证
- TPU-MLIR系列讲解(十四):Pattern Rewriting
- TPU-MLIR系列讲解(十五):模型适配
- TPU-MLIR系列讲解(十六):图优化
- ep1|TPU-MLIR Introduction AI Compiler
- TPU-MLIR Ep2 TPU-MLIR Overview
- TPU-MLIR Ep3 MLIR Brief Intro
- ep17 | TPU-MLIR Introduction :To ONNX Format
- TPU-MLIR线上分享会(一):论文讲解
- MegCC 用模型编译的方式实现超轻量端上高性能推理
- 陈天奇 机器学习课程
- AI-Compiler科普——TVM的使用讲解
- TVM流程梳理
- TVM-Realy流程梳理
- AI编译器后端优化介绍
- 算子的计算和调度
- 算子优化的手工方式
- 算子循环优化
- 指令和存储优化
- Auto Tuning原理
- TVM简介
- TVM自动调度算法AutoTVM
- ANSOR:为深度学习生成高性能张量程序
- TVM 编译流程与中间表示分析(一)
- TVM 编译流程与中间表示分析(二)
- TVM 学习指南(个人版)
- 白杨:TVM源语-Compute篇
- MLSys 15-884: Course Introduction
- OSDI 2021 PET 论文解读(代码生成相关工作)
- Buddy-MLIR 项目详解(入门 MLIR 极佳选择)
- 【社区实践】为 TVM 新增 OneFlow 前端
- 【TVM 三代优化巡礼】在X86上将普通的矩阵乘法算子提速90倍
- 【论文解读】基于MLIR生成矩阵乘法的高性能GPU代码,性能持平cuBLAS
- 【从零开始学深度学习编译器】二十,MLIR的Pattern Rewrite机制
- 【从零开始学深度学习编译器】十九,MLIR的Pass机制实践
- MLIR:摩尔定律终结的编译器基础结构 论文解读
- 【从零开始学深度学习编译器】十八,MLIR中的Interfaces
- 【用沐神的方法阅读PyTorch FX论文】
- 【以OneFlow为例探索MLIR的实际开发流程】
- 【从零开始学深度学习编译器】十七,MLIR ODS要点总结下篇
- 【从零开始学深度学习编译器】十六,MLIR ODS要点总结上篇
- 【从零开始学深度学习编译器】十五,MLIR Toy Tutorials学习笔记之Lowering到LLVM IR
- 【从零开始学深度学习编译器】十四,MLIR Toy Tutorials学习笔记之部分Lowering
- 【从零开始学深度学习编译器】十三,如何在MLIR里面写Pass?
- 【从零开始学深度学习编译器】十二,MLIR Toy Tutorials学习笔记一
- 【从零开始学深度学习编译器】十一,初识MLIR
- 可以让深度学习编译器来指导算子优化吗
- 【从零开始学深度学习编译器】十,TVM的整体把握
- Ansor论文阅读笔记&&论文翻译
- 【从零开始学深度学习编译器】九,TVM的CodeGen流程
- 【从零开始学深度学习编译器】番外二,在Jetson Nano上玩TVM
- 【从零开始学深度学习编译器】八,TVM的算符融合以及如何使用TVM Pass Infra自定义Pass
- 【从零开始学深度学习编译器】七,万字长文入门TVM Pass
- 【从零开始学深度学习编译器】六,TVM的编译流程详解
- 【从零开始学深度学习编译器】五,TVM Relay以及Pass简介
- 【从零开始学深度学习编译器】番外一,Data Flow和Control Flow
- 【从零开始学深度学习编译器】四,解析TVM算子
- 【从零开始学TVM】三,基于ONNX模型结构了解TVM的前端
- 【从零开始学深度学习编译器】二,TVM中的scheduler
- 【从零开始学深度学习编译器】一,深度学习编译器及TVM 介绍
- LLVM Tutorial
- miniSysY 编译实验课程,学习LLVM的中文入门资料
- 中科院 LLVM每日谈专栏
- 使用LLVM实现一门语言(一)Lexer
- 使用LLVM实现一门语言(二)Parser
- 使用LLVM实现一门语言(三)Code Generation to LLVM IR
- 使用LLVM实现一门语言(四)Optimizer
- 使用LLVM实现一门语言(五)Adding a JIT Compiler
- 使用LLVM实现一门语言(六)SSA
- 使用LLVM实现一门语言(七)Control Flow
- 使用LLVM实现一门语言(八)User-defined Operators
- 使用LLVM实现一门语言(九)Mutable Variables
- 深度学习编译器 TVM 代码串讲
- TVM Overview
- TVM - Relay IR计算图可视化
- TVM - 代码生成流程
- TVM/VTA代码生成流程
- tvm算子优化schedule(一)--CPU篇
- tvm算子优化schedule(二)--GPU篇
- TVM Runtime System 概述
- TVM PackedFunc实现机制
- 深入理解TVM:Python/C++互调(上)
- Round-tripping objects through the FFI
- TVM 自底向上(一):基本框架和概念
- TVM 自底向上(二):TIR 的概念和编译原理
- TVM 自底向上(三):TE 的概念和编译原理
- TVM 自底向上(四):TE/TIR Schedule 的原理
- 深入理解TVM专栏,主要是对部分codebase的解读
- tvm schedule详细举例
- TVM - 代码生成流程
- Relax: TVM 的下一代图层级 IR
- TVM之Tensor数据结构解读
- TVM之设计模式解读(一)--visitor模式
- TVM之设计模式解读(二)--责任链模式
- TVM之TIR相关数据结构
- TVM之设计模式解读(三)-单例模式,模板方法模式
- TVM之tir 转换成llvm ir
- TVM之graph_runtime
- TVM之relay.build流程解读
- TVM学习(一)
- TVM学习(二):算符融合
- TVM学习(三)编译流程
- TVM学习(四)codegen
- TVM学习(五)schedule
- TVM学习(六)细读前端
- TVM学习(七)算子
- TVM学习(八)pass总结
- TVM学习(九)codegen中的内存申请
- TVM学习(十)从relay到TOPI
- TVM TensorIR 浅析
- TVM图编译器NNVM简单探究
- TVM图编译器Relay简单探究
- 基于TensorIR生成mma指令并实现16x16x4矩阵乘
- 基于TVM的PTX Tensor Core汇编代码生成
- 一个tvm(te)实现的cutlass efficient gemm
- TIR Script CUTLASS Efficient Gemm
- TVM系列「一」TVM概览
- TVM系列「二」TVM学习资源
- TVM系列「三」TVM官方文档的结构
- TVM系列「四」TVM的使用:compute+schedule双剑合璧
- TVM系列「五」TVM整体架构及其代码生成
- TVM系列「六」Relay IR与Relay Pass
- TVM系列「七」AutoTVM(AutoTune)
- TVM系列「八」AutoScheduler「Ansor」
- 机器学习编译器代码生成相关 MLIR Dialect
- 编译器与中间表示: LLVM IR, SPIR-V, 以及 MLIR
- MLIR Vector Dialect 以及 Patterns
- MLIR Linalg Dialect 以及 Patterns
- 向外借力:Pluto助力MLIR编译器的多面体优化
- IREE编译流程解析
- IREE编译流程解析(一)
- IREE编译流程解析(二)
- IREE编译流程解析(三)
- IREE编译流程解析(四)
- IREE编译流程解析(五)
- IREE编译流程解析(六)
- megcc 开箱评测
开拓眼界...
- Glenside : 如何自动发现im2col布局转换?
- 基于Halide自动生成Kernel Fusion & Tiling
- AKG: 使用post-tiling fusion策略完成无副作用的内存优化
- [教程翻译]Polyhedral Tutorials
- 带宽受限下的DSA后端优化
- Equality Saturation优化在AI编译器中遇到的挑战
- DSA后端Compute Schedule与Buffer Schedule
- ASPLOS,我的初体验
- 读You and Your Research笔记
- [阅读笔记]AStitch @ASPLOS 2022
- [阅读笔记]RAKE @ASPLOS 2022
- [阅读笔记]NASA @ISCA 2021
- [阅读笔记]BOLT @MLSys 2022
- [阅读笔记]Alpa/Parax @OSDI 2022
- [阅读笔记]SIMD^2 ISCA 2022
- AMOS ISCA 2022
- [阅读笔记]PCCS MICRO 2021
- [阅读笔记]Planaria@MICRO 2020
- Chimera HPCA 2023
- 在MacBook Pro 2019上优化GEMM
2021年 2 月份发布了 DeepSpeed。这是一个开源深度学习训练优化库,包含的一个新的显存优化技术—— ZeRO(零冗余优化器),通过扩大规模,提升速度,控制成本,提升可用性,极大地推进了大模型训练能力。DeepSpeed 已经帮助研究人员,开发了图灵自然语言生成模型( Turing-NLG),在发表时,为世界上最大的语言模型(拥有 170 亿参数),有着最佳的精度。在2021年 5 月份发布了 ZeRO-2——支持有着 2000 亿参数的模型训练,与最新技术相比,训练速度可达 10 倍——系列计算、IO 和收敛优化功能,从而助力最快速的 BERT 训练。自那时起,持续高速进行创新,不断突破深度学习模型训练的速度和规模的边界。
这些进展不仅会推动深度学习训练走向极致,同时也让这份技术的使用范围更加广泛——上至数据科学家们在超算上训练,下至在低端集群甚至仅仅一张 GPU 上训练。具体来说,DeepSpeed 加入了 4 项系统性新技术来进一步拓展 AI at Scale 倡议。推动了微软的AI产品与平台的创新。这些技术提供了极为高效的计算、显存和通信的利用效率,并助力训练有着十亿至万亿量级参数的模型。支持超长输入序列,无论在单卡GPU、千卡GPU的高端集群上,还是在慢速以太网的低端集群上,均可以使用。
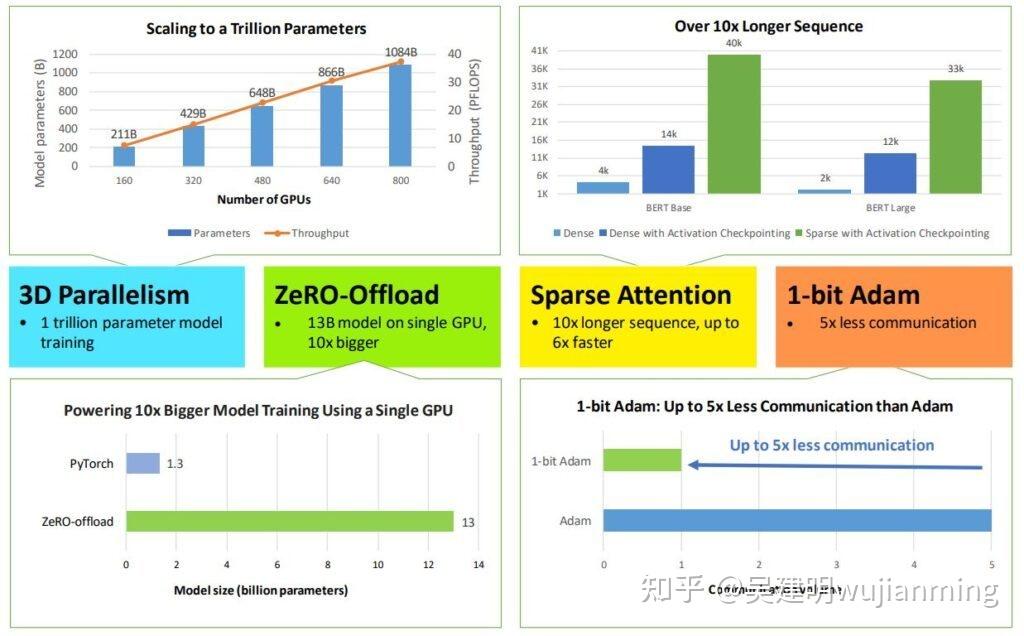
- 用 3D 并行化实现万亿参数模型训练: DeepSpeed 实现了三种并行方法的灵活组合:ZeRO 支持的数据并行,流水线并行和张量切片模型并行。3D 并行性适应了不同工作负载的需求,支持具有万亿参数的超大型模型,实现了近乎完美的显存扩展性和吞吐量扩展效率。提高的通信效率,使用户可以在网络带宽有限的常规群集上,以 2-7 倍的速度训练有数十亿参数的模型。
- ZeRO-Offload 使 GPU 单卡,能够训练 10 倍大的模型: 为了同时利用 CPU 和 GPU 内存来训练大型模型,扩展了 ZeRO-2。用户在使用带有单张英伟达 V100 GPU 的机器时,可以在不耗尽显存的情况下,运行多达 130 亿个参数的模型,模型规模扩展至现有方法的10倍,保持有竞争力的吞吐量。此功能使数十亿参数的模型训练,更加大众化,,并为许多深度学习从业人员,打开了一扇探索更大更好的模型的窗户。
- 通过 DeepSpeed Sparse Attention,用6倍速度执行10倍长的序列: DeepSpeed提供了稀疏 attention kernel ——一种工具性技术,可支持长序列的模型输入,包括文本输入,图像输入和语音输入。与经典的稠密 Transformer 相比,支持的输入序列长一个数量级,在保持相当的精度下,获得最高 6 倍的执行速度提升。还比最新的稀疏实现快 1.5–3 倍。稀疏 kernel 灵活支持稀疏格式,使用户能够通过自定义稀疏结构进行创新。
- 1 比特 Adam 减少 5 倍通信量: Adam 是一个在大规模深度学习模型训练场景下的,有效的(也许是最广为应用的)优化器。与通信效率优化算法往往不兼容。在跨设备进行分布式扩展时,通信开销可能成为瓶颈。推出了一种 1 比特 Adam 新算法,高效实现。该算法最多可减少 5 倍通信量,实现了与Adam相似的收敛率。在通信受限的场景下,观察到分布式训练速度,提升了 3.5 倍,这使得该算法,可以扩展到不同类型的 GPU 群集和网络环境。
a screenshot of a cell phone
将深入探究这 4 项技术。已经将这些激动人心的优化技术公布在了开源项目 DeepSpeed中。
随着现代 GPU 群集上计算量的快速增长,训练具有惊人的功能的、强大的万亿参数模型,不再是遥不可及的,可能在不久的将来就能实现。DeepSpeed 结合了三项强大的技术,可以训练数万亿规模的模型,扩展到数千个 GPU:数据并行训练,模型并行训练和流水线并行训练。这三者的共生让深度学习训练的规模,远远超出了单独使用每种策略。3D 并行解决了训练万亿参数模型的两个基本挑战:显存效率和计算效率。DeepSpeed 可以扩展至在显存中,放下最巨大的模型,不会牺牲速度。
了解训练巨大模型的显存和计算效率的挑战
显存效率:训练万亿参数模型所需的显存,远远超出了单张 GPU 的显存大小。在使用 Adam 优化器,进行混合精度训练时,存储模型状态量(参数、梯度和优化器状态量)需要约 16TB 的显存。最先进的英伟达 A100 GPU 只有 40 GB 的显存。仅仅为了存储模型状态,需要 400 张这样的 GPU。
激活函数额外消耗的显存,随 batch 大小而增加。batch 设置为1的情况下,训练万亿参数模型,产生超过 1 TB 的激活函数用的显存(后文称为激活显存)。用 checkpoint 处理激活显存,用计算换显存,可以将显存减少到大约20 GB,对于训练而言,仍然过高了。
必须在多个 GPU 设备之间,有效地划分模型状态量和激活显存,才能让这种大模型,在不耗尽显存的情况下,开始训练。
计算效率:经估算端到端训练一个万亿参数的模型,大约需要 5000 Zflops(即 5 后面带有 24 个零;这个估算结果基于 OpenAI 的研究 law of scaling)。训练一个模型需要 4000 张 A100,以 50% 的计算效率运行大约 100 天。
尽管大型超级计算 GPU 集群,可以拥有超过 4000 个 GPU,但是由于 batch 大小的限制,要在这种规模上实现高计算效率,仍然是一项挑战。计算效率随着计算时间,对通信时间的比例的增加而增加。该比例与 batch 大小成正比。训练模型的 batch 大小,有一个上限——超过这个上限,收敛情况会明显变差。
实际上最大的模型之一,GPT-3 的训练 batch 大小约 1500。如果使用大约 4000 张 GPU, 即使可以自由设置 batch 大小为 4000,每张卡上的 batch 大小,也只有 1,这将影响扩展性。
理解数据并行、模型并行和流水线并行之间的权衡
数据并行是深度学习中的一种普遍使用的技术。每批输入的训练数据,都在数据并行的 worker 之间平分。反向传播后,需要通信规约梯度,保证优化器在各个 worker 上进行相同的更新。数据并行性,具有几个明显的优势,包括计算效率高和实现起来工作量小。数据并行的 batch 大小,随 worker 数量提高,往往无法在不影响收敛性的情况下,一直增加 batch 大小。
- 显存效率:数据并行会在所有 worker 之间,进行模型和优化器的复制,显存效率不高。DeepSpeed 开发了 ZeRO ,一系列用于提高数据并行的显存效率的优化器。依赖于 ZeRO 的 1 阶段,在 worker 之间划分优化器状态量,减少冗余。
- 计算效率:随着提高并行度,每个 worker 执行的计算量是恒定的。数据并行,在小规模上实现近乎线性扩展。在 worker 之间规约梯度的通信开销,跟模型大小成正相关,当模型很大或通信带宽很低时,计算效率会受限。。梯度累积是一种均摊通信成本的一种常用策略。进一步增加batch大小,在本地使用 micro-batch,多次进行正向和反向传播积累梯度后,进行梯度规约和优化器更新。
模型并行是包含范围很广的一类技术。在多个 worker 之间,划分模型的各个层。模型并行性的计算和通信因模型结构而异,在实现上有很大的工作量。DeepSpeed 借用了英伟达的 Megatron-LM,基于 Transformer 的语言模型,提供大规模模型并行功能。模型并行根据 worker 数量,成比例地减少显存使用量,也是这三种并行度中显存效率最高的。代价是计算效率最低。
- 显存效率:模型并行会根据 worker 数量,成比例地减少显存使用量。减少单个网络层的激活显存的唯一方法。DeepSpeed 通过在模型并行 worker 之间,划分激活显存,进一步提高显存效率。
- 计算效率:每次前向和反向传播需要额外通信激活值,模型并行的计算效率很低。模型并行需要高通信带宽,不能很好地扩展到通信带宽受限的节点。每个模型并行worker,都会减少每个通信阶段之间执行的计算量,影响计算效率。模型并行性通常与数据并行性结合使用,在内存和计算效率之间进行权衡。
流水线并行训练引擎,包含在了这次发布的DeepSpeed中!流水线并行将模型的各层划分,可以并行处理。当完成一个 micro-batch 的正向传递时,激活内存将被通信至流水线的下一个阶段。当下一阶段完成反向传播时,将通过管道反向通信梯度。必须同时计算多个 micro-batch,确保流水线的各个阶段能并行计算。已经开发出了几种用于权衡内存和计算效率收敛行为的方法,例如 PipeDream。DeepSpeed通过梯度累积来实现并行,保持与传统数据并行和模型并行训练,在相同的总 batch 大小下收敛。
- 显存效率:流水线并行减少的显存与流水线的阶段数成正比,使模型的大小,可以随 worker 的数量线性扩展。流水线并行不会减少每一层的激活函数的显存占用量。每个 worker 必须存储,同时运行的各个 micro-batch激活值。导致流水线第一阶段的激活内存,与单个 mirco batch 的总激活内存,大致相同。一个万亿参数模型,需要为一个 micro batch,提供大约 19 GB 的显存的激活内存,几乎占到新推出的英伟达 A100 GPU 总显存的一半。
- 计算效率:流水线并行具有最低的通信量,通信量只和在各阶段边界的各层的激活值大小成正比。但是不能无限扩展。像模型并行一样,增加流水线大小,会减少每个流水线阶段的计算量,降低计算与通信的比率。如果要实现好的计算效率,流水线并行,要求其每个阶段的计算负载完美均衡。
此外,流水线并行性,在每个 batch 的开始和结束时,因为需要重新填充,或排空流水线,产生 bubble overhead。使用流水线阶段数的 4 倍或 8 倍的梯度,累积步骤(以及 batch 大小)进行训练,相较于只有一个流水线阶段,分别达到了 81% 和 90% 的扩展性。
数据,模型和流水线并行,在提高内存和计算效率方面,均起到特定的作用。图 1 说明了 3D 策略。
显存效率:先将模型的各层,划分到不同的流水线阶段,把每个阶段的层通过模型并行,进行划分。这种 2D 组合同时减少了模型、优化器和激活函数所消耗的内存。不能在不引入通信开销的情况下,无限划分模型,通信开销会限制计算效率。
计算效率:为了在不牺牲计算效率,将 worker 数量扩展至超出模型和流水线并行规模,使用了 ZeRO 支持的数据并行功能(ZeRO-DP)。ZeRO-DP 不仅可以通过划分优化器状态量,进一步提高显存利用效率,通过利用基于通信拓扑的映射关系,以最小的通信开销,扩展到任意数量的 GPU。
基于通信拓扑的 3D 映射(图2):通过利用两个关键的架构属性,将 3D 并行中的每个维度,仔细映射到 worker 上,实现最大的计算效率。
- 优化节点内和节点间的通信带宽:模型并行是这三种策略中通信开销最大的,优先考虑将模型并行 worker 组放置在节点内,利用更大的节点内带宽。基于英伟达 Megatron-LM,进行了张量切分式的模型并行。当模型并行组不占满节点内的所有 worker 时,选择将数据并行组放置在节点内。不然,就跨节点进行数据并行。流水线并行的通信量最低,可以跨节点调度流水线的各个阶段,不受通信带宽的限制。
- 通过并行通信增大带宽:每个数据并行组,需要通信的梯度量,随着流水线和模型并行的规模线性减小,总通信量少于单纯使用数据并行。此外,每个数据并行组,在局部的一小部分 worker 内部,独立进行通信,组间通信可以相互并行。通过减少通信量和增加局部性与并行性,数据并行通信的有效带宽被增大了。
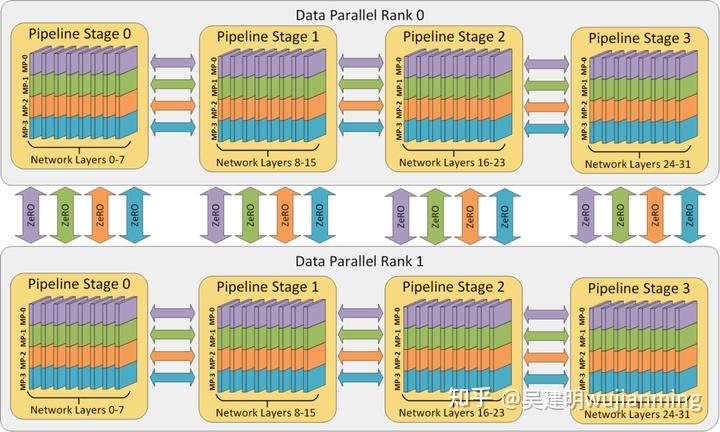
该图显示了一个有 32 个 worker 进行 3D 并行的例子。神经网络的各层分为四个流水线阶段。每个流水线阶段中的层在四个模型并行 worker 之间进一步划分。最后,每个流水线阶段有两个数据并行实例,且 ZeRO 在这 2 个副本之间划分优化器状态量。
图 1:一个有 32 个 worker 进行 3D 并行的例子。神经网络的各层分为四个流水线阶段。每个流水线阶段中的层在四个模型并行 worker 之间,进一步划分。每个流水线阶段,有两个数据并行实例,ZeRO 在这 2 个副本之间,划分优化器状态量。
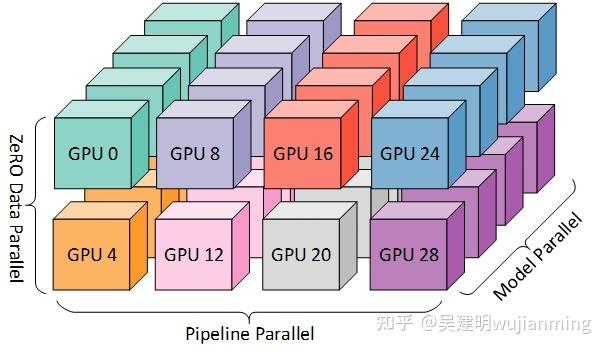
彩色块显示图 1 中的 worker 到八个节点(每个节点有四个 GPU)的系统上的 GPU 的映射。同一颜色的 GPU 在同一节点上。
图 2:图 1 中的 worker 到八个节点(每个节点有四个 GPU)的系统上的 GPU 的映射。同一颜色的 GPU 在同一节点上。
了解关于 3D 并行训练万亿参数模型的更多信息
使用 8 路模型并行,64 路流水线并行和 8 路数据并行,在 4096 个英伟达 A100 GPU 上,扩展训练一个万亿参数模型。
通过结合模型并行和流水线并行,3D 并行可实现出色的内存效率和跨多个节点的高效计算效率。模型并行性,提高了节点内的激活内存和模型状态量的存储效率,流水线并行,相较于仅使用模型并行,可以在不牺牲计算效率的情况下,跨节点高效存储模型状态。在 micro-batch 大小为 1 的万亿参数例子中,在使用激活值 checkpoint及上述 3D 并行后,模型状态量会消耗 30 GB 的显存,划分后的激活值消耗 2.5 GB 的内存。总显存占用为 32.5 GB,就能够使用具有 40 GB 内存的英伟达 A100 GPU,容纳和训练这样的模型了。
结合模型并行与流水线并行,可以使流水线并行在非常小的 batch 下,以最小的 bubble overhead,实现高计算效率。在 8 路模型并行下,每个模型使用 micro-batch 为 1 个微批处理,导致每个 GPU 的有效 micro-batch 大小为 1/8。使用 8 倍于管道并行度的梯度累加步骤,让每张 GPU 上的总累计 batch 大小为 1,流水并行处理,可以实现 90% 的计算效率。与数据并行性结合使用时,让 4096 张 GPU 上的总有效 batch 大小为 4096,仍然可以达到 90% 的流水线效率。
数据并行怎样影响计算效率呢?难道数据并行不是需要每张 GPU,都有大 batch 才能保持高效吗?
模型并行可以将每张GPU上的有效 batch 大小,减小到小于 1。使流水线并行,即使在小 batch 下,仍可以隐藏流水线 bubble overhead。通过跨节点使用流水线并行性,可以让流水线每个阶段的数据并行节点之间的独立进行通信,与其它流水线并行进行。实际上,在高端 GPU 集群中常见的,完全连接的网络拓扑中,对可用于数据并行训练的有效通信带宽,具有重要意义。流水线阶段中的每个节点,都可以与其对应的数据并行节点,并行通信,有效的通信带宽与流水线阶段数成正比。通过设置64个并行流水线,有效带宽将变为往返单个节点的带宽的 64 倍。流水线并行带给数据并行,如此大的有效带宽,使数据并行在计算与通信比率非常低的小 batch 情况下,实现高效扩展。
DeepSpeed 可以只用 800 张英伟达 V100 GPU,训练具有一个万亿参数的语言模型(图 3)。展示了模型大小和训练吞吐量,可以观察到显存和计算效率,随模型的大小的扩展线性增长。在各种配置中,在每个 GPU 上训练,大约 14 亿个参数,这是单个 GPU 在不耗尽内存的情况下,可以支持的最大模型大小,表明了完美的显存扩展性。获得了接近完美的线性计算效率扩展,每张 V100 GPU 的吞吐量为 47 Tflops。对于上述的硬件,这是令人印象深刻的扩展性和吞吐量。
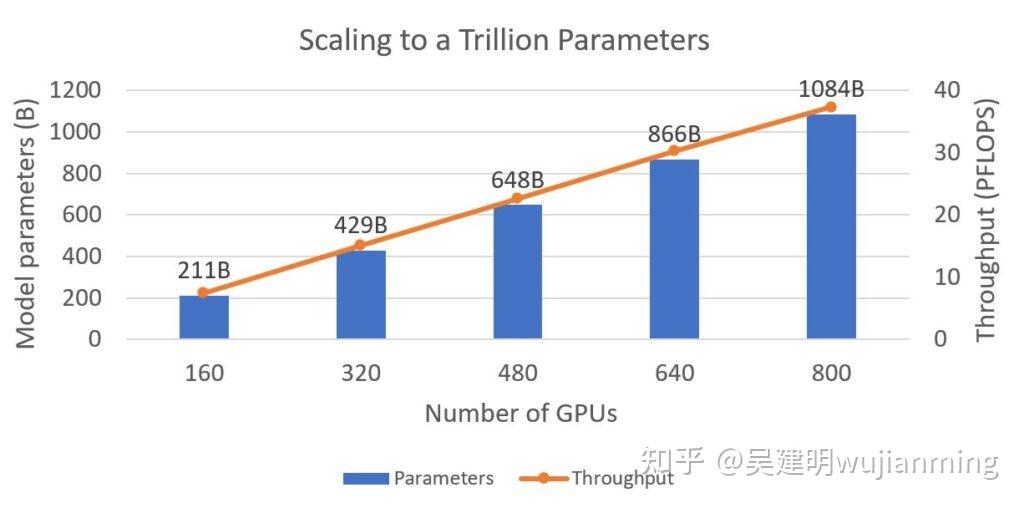
图3:模型大小(以十亿个参数为单位)和训练吞吐量(以 Pflops 为单位)随 GPU 数量变化趋势的图表。DeepSpeed 可以使用 800 张,具有 32 GB 内存的英伟达 V100 Tensor Core GPU,训练有 1 万亿个参数的模型。每种配置都使用 NVIDIA Megatron-LM 提供的,16路模型并行性,剩余的GPU,负责进行流水线并行。万亿参数模型,具有 298 层 Transformer,隐藏层大小为 17408,训练的序列长度为 2048,batch 大小 2048。对于较小的模型,根据 GPU 数量,按比例减少了 Transformer 层的数量和 batch 大小。
深入研究 3D 并行,如何加速训练 GPT-3 规模的模型
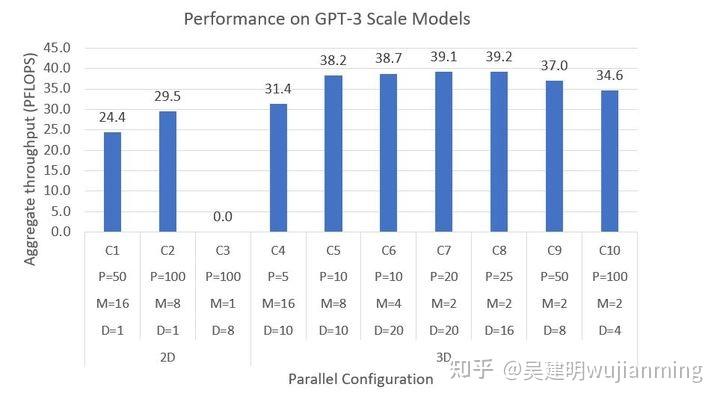
图 4:使用 2D 和 3D 并行,使用 800 个 GPU,训练具有 1800 亿参数的 GPT-3 规模模型的系统性能。模型具有 100 个 Transformer 层,隐藏层尺寸为 12288,有 96 个 attention head。训练使用的 batch 大小为 2048,序列长度为 2048。ZeRO-1可以跟数据并行结合使用。P、M 和 D 分别表示流水线,模型和数据并行维度。
在图 4 中,使用具有超过 1,750 亿个参数的最新 GPT-3 模型架构,作为 3D 并行性的基准:
- 首先评估了 2D 配置(C1-C3)。配置 C1 和 C2 仅使用流水线和模型并行——可以训练模型,由于过度分解模型,导致吞吐量较低,GPU 利用率较低。C3 尝试仅使用流水线和数据并行,不通过 Megatron 的模型并行,减少激活量,无法解决显存不足的问题。
- 3D 配置(C4-C10)依次增加了流水线并行度;中间的平衡了并行性的配置,实现最佳性能,实现了显存,计算和通信效率三高。
- 最佳的 3D 方法,每个GPU可实现 49 Tflops,超过硬件的理论峰值的 40%。
混合并行如何在低带宽集群上,7 倍加速训练 GPT-2
训练了一个 15 亿参数的 GPT-2 模型,在图 5,展示了混合并行的通信优势。为了突出展示训练的通信阶段,训练在节点间带宽较低的四节点的群集上进行:
- 模型并行在这种情况下没有优势,因为模型较小,节点内带宽较低。
- 流水线并行的通信量,比配置数据和模型并行的情况,小一个数量级。在 batch 较小时,训练速度快 7 倍。
- 数据并行使用通过梯度累积增加 batch 大小,均摊通信开销,在更大的 batch 大小下,配置了流水线并行的情况的性能,仍是数据并行的两倍。
- 混合流水线和数据并行配置,通过将数据并行组限制在节点内的 GPU 上,避免了梯度通信瓶颈,因此梯度通信受益于更快的节点内带宽。
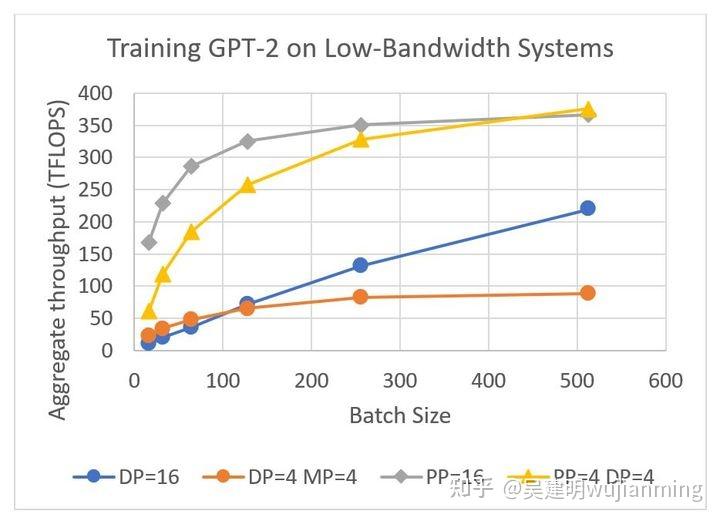
图 5:在训练序列长度为 1024 的 GPT-2(1.5B 参数)时,吞吐量与 batch 大小的关系。使用四个节点,每个节点配备四个具有 16 GB 内存的 V100 GPU 训练。GPU 之间用每秒 50 Gbps 的节点内带宽和 4 Gbps 的节点间带宽连接。DP 表示启用 ZeRO-1 的数据并行性。所有方法都通过增加梯度累积的步数,扩展批量大小。
ZeRO-Offload 通过同时利用GPU和宿主机 CPU 的计算和存储资源,提升了较少的 GPU 资源下,可以高效训练的最大模型规模。在单张 V100 上,进行最高至 1300 亿参数的模型训练,10 倍于当前最高水平,保持每 GPU 30Tflop 的高训练吞吐量。
通过使单 GPU,具备训练数十亿参数的模型的能力,ZeRO-Offload 让大模型训练变得亲民,让硬件资源有限的深度学习,从业者也能参与其中。
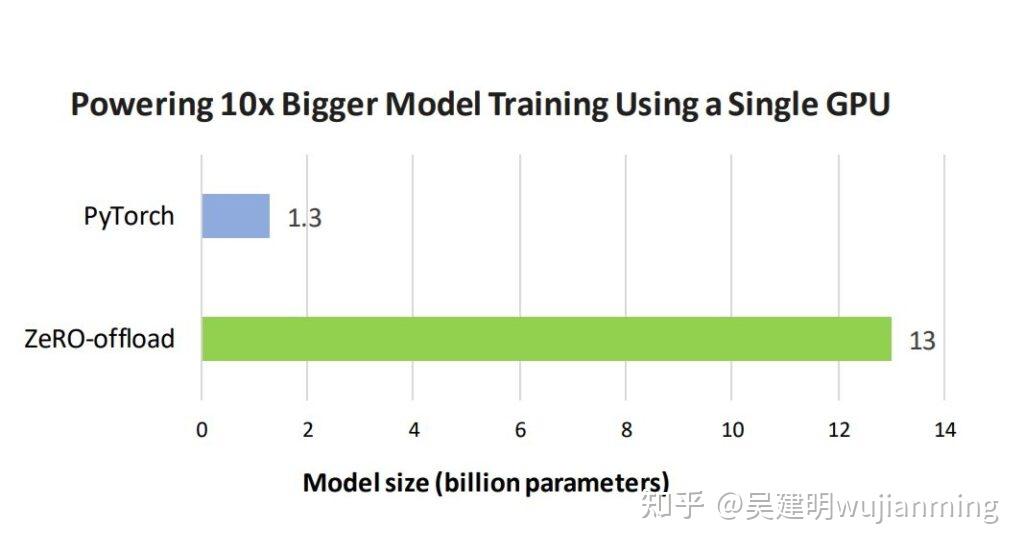
在单 GPU 上使用默认的 PyTorch 和 ZeRO-Offload,能训练的最大模型规模的柱状图。
图 6:可以在单 GPU 上使用默认的 PyTorch 和 ZeRO-Offload 训练的最大的模型规模。
ZeRO-Offload 背后的核心技术,在 ZeRO-2 的基础上,将优化器状态和梯度,卸至 CPU 内存。让 ZeRO-Offload 能最大程度,降低拷贝至 CPU 导致的计算效率损失,达到和 ZeRO-2 相同,甚至有时超过的效率。下图展示了 Zero-OffLoad 的架构:
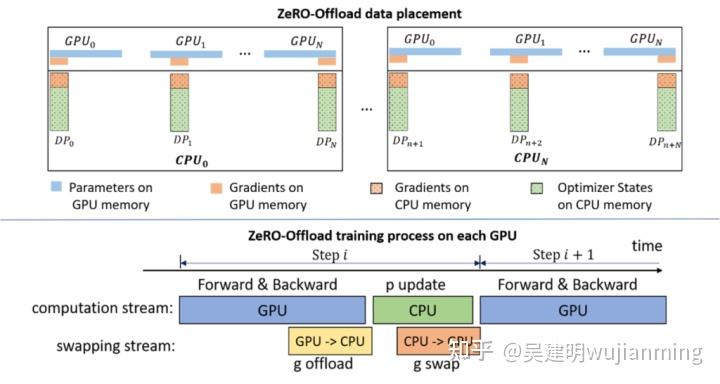
图7: ZeRO-Offload 概述。
了解 ZeRO-Offload 是如何在单GPU上,训练数十亿参数模型的
训练 GPT 和 T5,这样有数十亿参数的模型,需要多个 GPU 来存储模型和状态量。大模型训练大多通过跨 GPU 的模型并行,解决显存限制问题。最近,发布了 ZeRO,一个高效利用显存的优化器,将模型状态量(优化器状态量、梯度和模型参数),分布在多个并行 GPU 上,让数十亿参数模型,在不使用模型并行的情况下,进行训练。ZeRO 还是需要大量数据并行的 GPU,保存划分后的模型状态量,只有少数人,有条件进行这种模型训练。
ZeRO-Offload 让单 GPU 可以进行大模型训练,使这种训练变得平民化。为了在不使用多个 GPU 的情况下,训练数十亿个参数的模型,ZeRO-Offload 继承了 ZeRO-2 的划分优化器状态量和梯度的方法。与ZeRO-2 不同,ZeRO-Offload没有在每个 GPU 上保存一部分优化器状态量和梯度,把两者都移到了本机内存上。Optimizer 状态,在整体训练过程中,都保存在内存中。梯度则是在反向计算过程中,在 GPU 上进行计算,通过 reduce-scatter 进行平均,每个数据并行进程,把平均后的梯度,卸到 CPU 上(图7中的 g offload),弃掉不属于自己负责的部分。
一旦梯度到了 CPU 上,划分后的优化状态量,就会并行地在 CPU 上,进行更新(图7中的 p update)。在更新进行完后,划分后的参数就被移回GPU并用 all gather 操作进行更新 (图7中的 g swap)。Zero-Offload 也通过使用不同 CUDA stream,重叠通信(如 g offload 和 g swap)和计算(如反向传播和 p update),提高训练效率。
从模型规模,训练速度和扩展性看 ZeRO-Offload 的优势
10 倍模型扩展:在单张 32GB V100 GPU 上,图 6 显示 PyTorch 能最多训练有 13 亿个参数的模型,ZeRO-Offload 能训练 130 亿个参数的模型, PyTorch 的 10 倍。ZeRO-Offload 在整个训练过程中,将消耗了大部分 GPU 显存的优化器状态,保留在本机内存中,在反向传播过程中,将计算出来的梯度移至 CPU。节省的 GPU 显存,可用于训练更大的模型。
高效的训练吞吐量:如图 8 所示,在训练 100 亿参数模型时,即使仅使用单个 GPU 进行训练,使用 ZeRO-Offload,可让每个 GPU 有超过 30 Tflops 的吞吐量,吞吐量随 GPU 数量增长,呈近完美的线性增长。
ZeRO-Offload 是 ZeRO-2 的完美补充,支持在少量 GPU 上,高效训练大型模型。通过利用 CPU 内存,减少了模型所需的 GPU 显存,ZeRO-Offload 让在 1 到 16 个 GPU,训练大模型变得可行。在 32 个 GPU 上,ZeRO-Offload 的性能,略高于 ZeRO-2; 性能提升来源于 ZeRO-Offload 节省的 GPU 显存,可以在更大 batch 下,训练了模型,尽管存在拷贝至 CPU 的开销,GPU 计算效率仍然可以提高。在有更多的 GPU(例如 64 和 128)的情况下,ZeRO-2 的性能,优于 ZeRO-Offload,两者都可以运行类似大小的batch,ZeRO-2 没有将数据移至 CPU 的开销,GPU 上进行优化器更新,比 CPU 上快得多。总之,ZeRO-Offload 是 ZeRO-2 的补充,扩展了 ZeRO 家族的优化范围,从单台设备到数千台设备,有大型模型训练的优化方案。
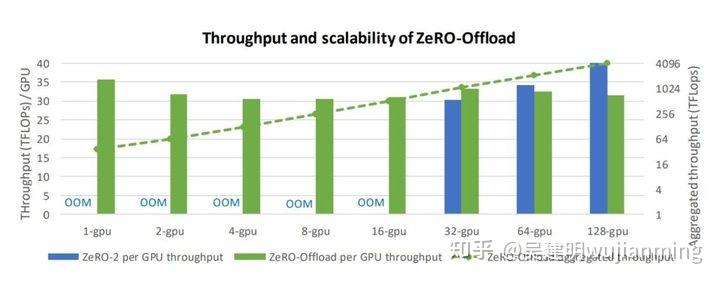
使用 ZeRO-Offload 和 ZeRO-2 在 128 张 GPU 上,训练有 100 亿参数的 GPT-2 模型的的吞吐量的柱状图。
图 8:使用 128 张 GPU,训练 100 亿参数 GPT-2 模型的 ZeRO-Offload 和 ZeRO-2 的训练吞吐量比较。
基于注意力机制的深度学习模型(例如,Transformers),在捕获输入序列中的 token 之间的关系(即使是两者之间距离很长)方面,非常有效。与文本,图像和语音相关的输入配合使用。这些输入的序列长度可至数千 token。注意力模块有效地捕获了长序列内的依赖关系,对长序列输入的支持,计算量和显存的限制。计算量和显存需求,关于序列长度\\(n\\)呈二次方级增长。
为了解决此限制,DeepSpeed 提供了一套稀疏注意力 kernel——一种工具性技术,通过块状稀疏计算,将注意力计算的计算和显存需求,降低几个数量级。这套工具不仅缓解了注意力计算的内存瓶颈,稀疏计算非常高效。API 可以方便地集成进,任何基于 Transformer 的模型。除了提供各种稀疏结构外,可以灵活处理任何用户,自定义的块状稀疏结构。
稀疏注意力(SA)可以设计计算,靠近的 token 之间的局部注意力,或通过使用局部注意力计算,得到 summary token,进而得到全局注意力。SA 既支持随机注意力,也支持局部、全局和随机注意力的任意组合,如图 10 中的蓝色,橙色和绿色块。使SA将内存占用减小到\\(O(wn)\\),其中1\\(<w≤n \\)是一个参数,取决于注意力结构。
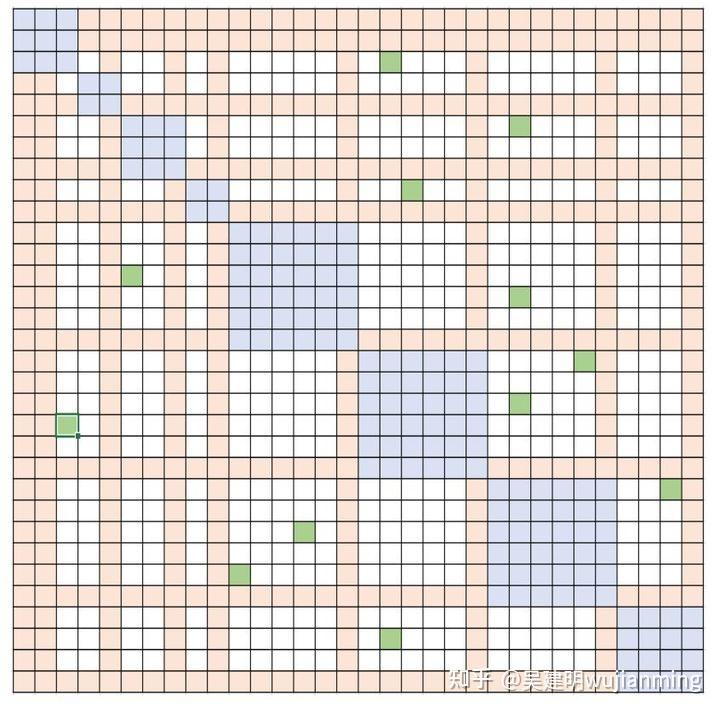
彩色小方块显示可变的稀疏度结构
图 10:可变稀疏结构
在 GPU 上的高效实现:尽管稀疏注意力的基本实现,节省显存,但在计算上,可能会比稠密计算要差。稀疏数据导致了内存访问的分散性。开发高效的稀疏内核,通常是颇具挑战性的,尤其是在 GPU 上。DeepSpeed 提供了在 Triton 中开发的高效的稀疏注意力 kernel。这些 kernel 呈块状稀疏范式结构,实现对齐的内存访问,减少GPU线程分支平衡处理器上的工作负载。
系统性能:如图11所示,SA 支持 10 倍长的序列和最高 6.3 倍的计算提速。左图显示了可在 BERT-Base 和 BERT-Large 中,运行的最长序列长度。实验有以下三种设置:稠密模式,具有激活 checkpoint 的稠密模式和具有激活 checkpoint 的稀疏(SA)模式。与 BERT-Base 和 BERT-Large 的稠密模式相比,SA 的序列分别长 10 倍和 16 倍。与稠密模式相比,SA 减少了总计算量,提高了训练速度:提高的效率随着序列长度的增加而提高,对于 BERT-Base 而言,提升速度高达 6.3 倍,对于 BERT-Large,高达 5.3 倍。
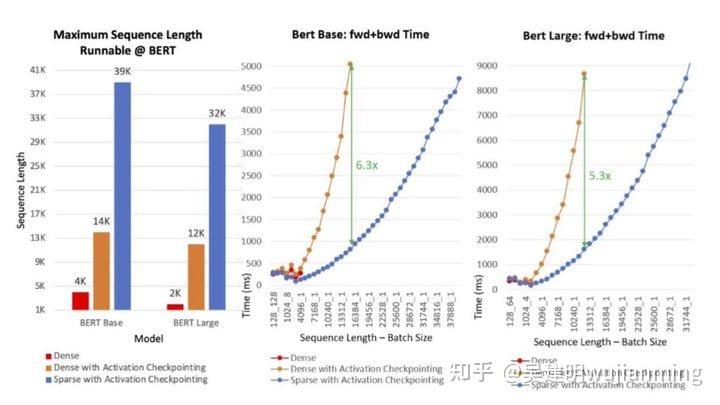
图11:BERT 模型的可支持的最大序列长度(左);在单英伟达 V100 GPU 上,训练具有不同序列长度的 BERT-Base(中)和 BERT-Large(右)的时间。
了解 SA 如何使其准确率与全稠密注意力相当,甚至比它更高
涉及稀疏注意力的相关工作(Sparse Transformer,Longformer,BigBird),均显示出比全注意力更高的准确性,与经验一致。除了降低内存开销和加快计算速度外,在生产模型中观察到 SA,有更高准确性,更快收敛的情况。下图说明了训练基于 BERT 的长文本,理解(序列长度 2048)生产模型的准确性。实验在以下三种设置中进行:从头开始进行稠密训练,从头开进行 SA 训练,从使用序列长度为 512 的密集型 checkpoint,继续进行 SA 训练。对于从头开始进行预训练,SA较于稠密设置收敛的速度更高,精度更好。时间和准确性,从用 SA 继续训练,预先训练好的 checkpoint 的效果,甚至更好。
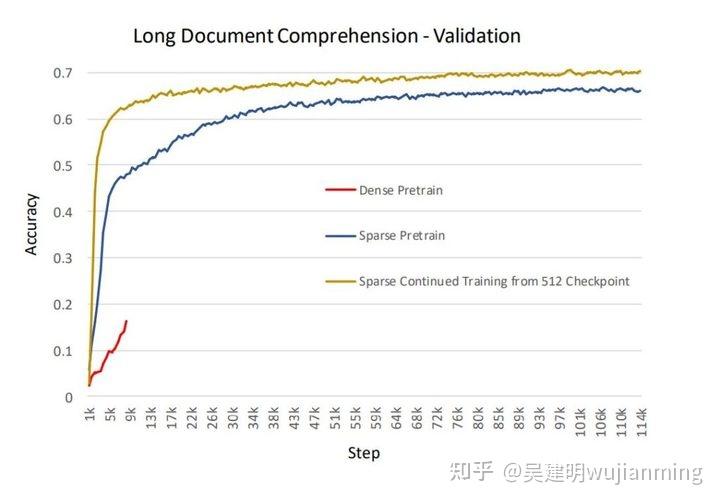
图12:长文本理解应用的准确性
了解 SA 与最新的 LongFormer 的比较情况
将 SA 与 Longformer(一种最新的稀疏结构及其实现)进行了比较。在实验中,SA 使用“Fixed”稀疏性。两种实现的准确性相当。在系统性能方面,SA在训练和推断方面均优于Longformer:
- 运行 Wikitext103 上的预训练MLM的速度,提高了 1.5 倍
- BERT-Base 的推理速度,提高3倍(batch 大小 1,序列长度 2,048)
处理任何块状稀疏结构的灵活性: DeepSpeed 稀疏注意力套件,不针对任何特定的稀疏结构,能有效支持模型研究人员探索任何块状稀疏结构。添加了流行的稀疏结构,例如 Fixed(来自OpenAI稀疏Transformer),[BigBird](https://arxiv.org/pdf/2007.14062 .pdf)(来自Google)和BSLongformer(AI2 Longformer的块稀疏实现)。定义了一个具有“可变”结构的模板,如图 10 所示,模板可用于简单地自定义任何随机,局部或全局注意力模式的块状稀疏结构。
大型模型(如 BERT 和 GPT-3)的扩展训练,需要基于模型设计,体系结构和系统功能的细致优化。从系统的角度来看,通信效率已成为主要的瓶颈,在使用标准 TCP 且网络带宽有限的商用系统上。
通信压缩是减少在此类系统上的训练时间的重要技术。压缩通信的最有效方法之一,误差补偿压缩,即使在1比特压缩下,可以提供稳定的收敛速度。但是,最新的误差补偿技术,仅适用于一些和梯度线性相关的简单优化器,随机梯度下降(SGD)和 Momentum SGD。这些技术无法和 Adam 之类的非线性优化器整合,在许多任务(包括训练类似 BERT 的模型)中,带来了最好的收敛率和精度。
对于像 Adam 之类的强大优化器,依赖于梯度的非线性特征(在方差项上),开发基于误差补偿的压缩技术,颇具挑战性的工作,限制了先进的通信压缩技术的实用价值。
理解经典压缩技术的背景
通信压缩的一种方法是1比特压缩,可以被表示为:
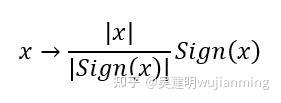
在这种压缩中,用 1 比特表示每个数字,将内存需求减少 32 倍。这种直接的方法会大大降低收敛速度,没什么实用价值。研究表明,通过使用误差补偿压缩,有望在通信压缩下,保证几乎相同的收敛率。
误差补偿的思想,可以概括为:1)进行压缩,2)记忆压缩误差,3)在下一次迭代中,把压缩误差加回来。对于 SGD,误差压缩相当于:
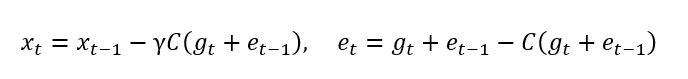
其中\\(C(?)\\)是1比特压缩算子。这种误差压缩的优点在于压缩误差的历史值\\(e_t\\)和\\(e_t-1\\)最终会相互抵消, 这使得:
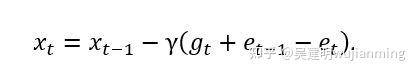
该策略已经被证明,适用于所有线性依赖于梯度的优化算法,例如 SGD 和 Momentum SGD。
了解将误差补偿应用于 Adam 的挑战
在下面提供了 Adam 算法的概述。更新规则如下:
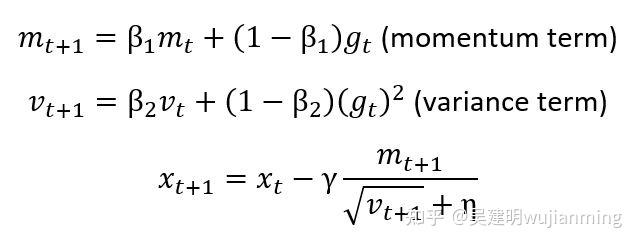
如上图的公式所示,方差项 \\(v_t\\) 和梯度 \\(g_t\\) 呈非线程关系。如果对 Adam 进行普通的误差补偿,发现(见图 13)Adam 将无法收敛。

图13:由于对梯度的非线性依赖,误差补偿压缩不适用于 Adam
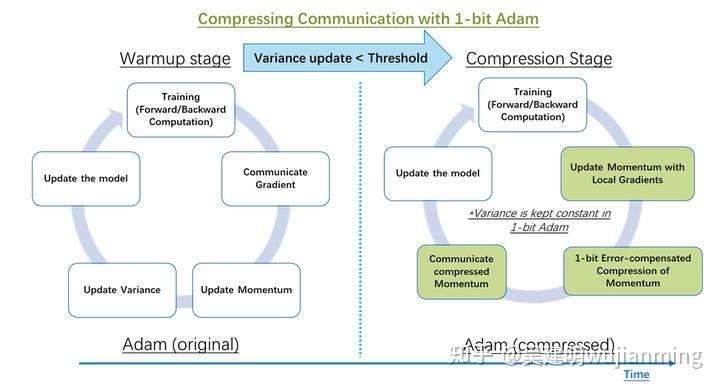
为了在使用 Adam 优化器时压缩通信,开发了 1 比特 Adam,通过预处理解决了梯度中的非线性依赖问题。观察到非线性项方差(\\(v_t\\))的变化幅度,在几个训练周期后显著降低,将 \\(v_t\\) 设置为常数不会改变收敛速度。1 位 Adam 优化器,由两部分组成(如图 14 所示):预热阶段,本质上就是原始的 Adam 算法。压缩阶段,使方差项保持恒定,将剩余的线性项(即动量)压缩为 1 位表示形式。
算法的压缩阶段,由阈值参数控制(如图 14 所示)。当检测到“方差”的变化,降至某个阈值以下时,切换到压缩阶段。研究表明,热身阶段,需要全部训练步骤的 15-20%。
进一步了解 1 比特 Adam 的底层机制
1 比特 Adam 的权重按以下公式进行更新。对于第 i 个 worker,在压缩阶段:

a screenshot of text
a screenshot of a cell phone
图 14:使用经典 Adam 算法和使用 1 比特压缩 Adam 算法,进行分布式训练的流程对比
除了算法上的挑战外,在训练系统中应用 1 比特 Adam,有两个系统挑战。首先,需要具备将动量转换为 1 比特表示形式的功能的高效 kernel。其次,需要高效的通信方案,在不同的 GPU 之间,传输压缩后的动量。压缩的目的是减少总体训练时间,使带宽受限的商品系统,用来训练大型模型。在 DeepSpeed 中,解决了这些具有挑战性的问题,针对在通信效率受限的系统上,进行训练的场景,对 1 比特 Adam 实现,进行了全面的优化。
1 比特 Adam 提供了和 Adam 相同的收敛能力,最多可以减少 5 倍的通信量,进行 BERT-Large 预训练任务时,可达最高 3.5 倍的吞吐量,用于 SQuAD fine-tuning 任务时,可达 2.7 倍的高吞吐量。端到端吞吐量的提高,来源于在压缩阶段观察到的 6.6 倍(图 15 左)和 6.2 倍(图 15 右)速度提升。1 位 Adam 优化器,在 40 Gb 以太网系统上的扩展性非常好,性能可与 Adam 在 40 Gb InfiniBand QDR 系统上的扩展性相媲美。基于 iPerf 基准,40 Gb 以太网上的有效带宽为 4.1 Gbps,基于 InfiniBand perftest 微基准,InfiniBand 提供了 32 Gbps 的近峰带宽。

图 15:NVIDIA V100 GPU 上的 BERT-Large 预训练(左)和 SQuAD fine-tuning(右)的 1 比特 Adam 扩展性。BERT 预训练的 batch 大小为 16/GPU,SQuAD fine-tuning 为 3/GPU。
深入研究 1 比特 Adam 的评测结果
与 Adam 相同的收敛性:使用 1 比特 Adam 的一个主要问题是收敛速度。发现在使用相同数量的训练样本时,1 比特 Adam,可以达到相同的收敛速度和相当的性能,见图 16。
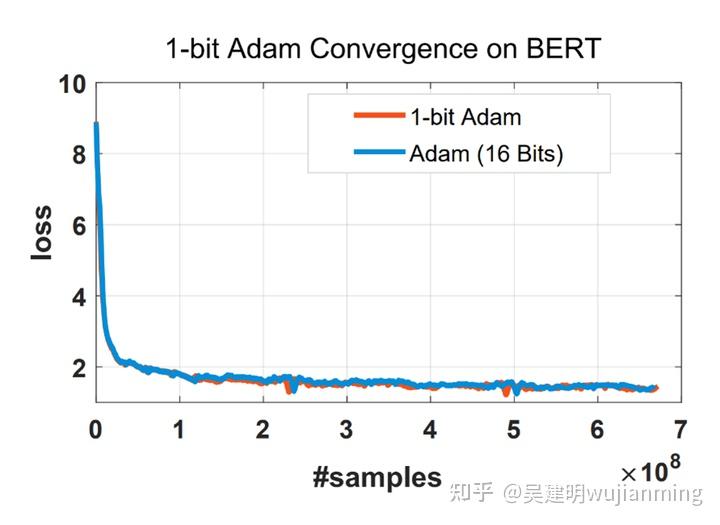
图 16:使用相同数量的训练样本,1 比特 Adam,可以像 Adam 一样收敛。
表 1 显示了 BERT-Base 和 BERT-Large 的详细结果。看到,对于未压缩和压缩情况,1 比特 Adam 的性能,均与原始模型相当,有些则优于原始模型。
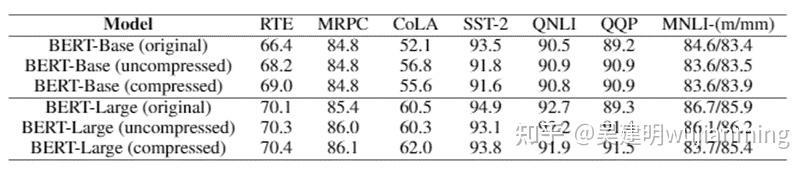
表 1:在各种测试任务上验证 1 比特 Adam 的正确性
最多可减少 5 倍的通信量: 1 比特 Adam,提供了与 Adam 相同的收敛能力,在压缩阶段(对于 16 位(FP16)训练),将通信量减少了 16 倍。 对于 BERT 预训练模型,观察到预热阶段,仅为端到端训练时间的 15%,总体通信减少了 5 倍。
原始 Adam 和 1 比特 Adam 的通信量之比的公式如下:
1 / (warmup + (1 – warmup)/16)
1 比特 Adam 使训练 BERT-Large 的速度快 3.5 倍: 提供了在两个具有有限带宽限制的系统上,训练 BERT-Large 的结果:1)40 Gbps 以太网(图 17 左)和 2)40 Gbps InfiniBand QDR(图 17 右)。在压缩阶段,发现使用以太网的系统吞吐量,提高了 6.6 倍,使用 InfiniBand的系统吞吐量,提高了 2 倍,端到端的速度(包括预热和压缩阶段),分别提高了 3.5 倍和 2.7 倍。1 比特 Adam 主要得益于通信量的减少(因为对动量通信的压缩实现),及自定义的 allreduce 操作,操作通过高效的 1 比特,无阻塞 gather 和一个 allgather 操作实现。
使用 LAMB 而不是 Adam 优化器,进行 BERT 预训练,通过增加总 batch 大小,减少通信量。1 比特的 Adam,避免了这种要求严格的超参数调参。根据经验,大 batch 下进行调参,通常会更加困难。此外,1 比特 Adam,对于临界批处理量较小(无法在大 batch 下良好收敛,例如许多 fine-tuning 任务)的工作也非常适用。
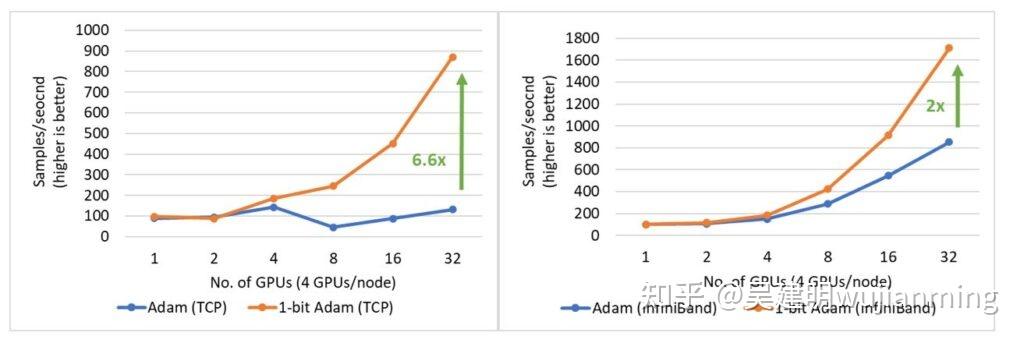
图 17:在压缩阶段,使用 1 比特 Adam 在 40 Gbps 以太网(左)和 InfiniBand(右)上,进行 BERT-Large 训练时的性能
1 比特 Adam 使 SQuAD fine-tuning 任务加速 2.7 倍: 1 比特 Adam,不仅在大规模训练任务上提供扩展性,而且在 SQuAD 微调之类的任务上,也有效果。如图 18 所示,1 比特 Adam,在基于以太网和基于 InfiniBand 的系统上很好地扩展,在基于以太网的系统上,提供高达 6.2 倍的高吞吐量(在压缩阶段),带来端到端的 2.7 倍提速(预热阶段占 25%,压缩阶段占 75%)。对于 SQuAD fine-tuning,观察到总 batch 大小为 96 时,F1 得分最高。 batch 大小大于此值降低收敛率,需要额外的超参数调整。为了扩展到 32 个 GPU,在每个 GPU 上运行值为 3-4 的小 batch。使得 fine-tuning 任务的通信强度大,难以扩展。1 比特 Adam,很好地解决了扩展性的难题,在不增大 batch 的情况下,减少了 3.4 倍的通信量,实现了 2.7 倍的端到端加速。
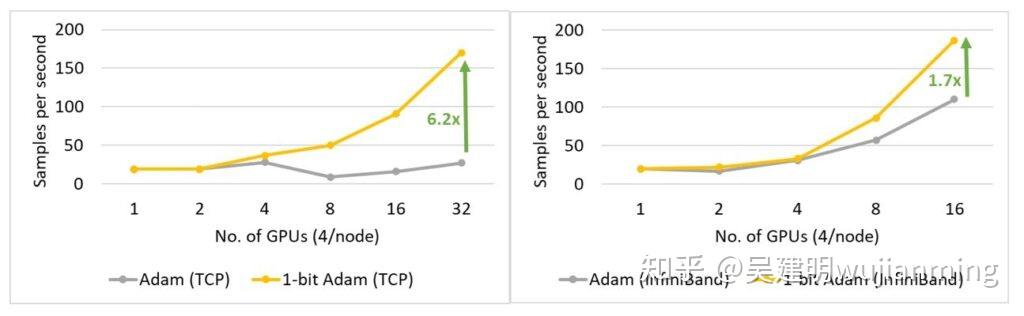
图 18:在 40 Gbps 以太网(左)和 InfiniBand(右)上的 SQuAD fine-tuning 任务中,使用 1 比特 Adam 时,压缩阶段的性能。
一群热衷于大规模系统性能优化的研究员和工程师——Samyam Rajbhandari, Jeff Rasley, Olatunji Ruwase, Reza Yazdani Aminabadi, Elton Zheng, Arash Ashari, Jing Zhao, Minjia Zhang, Niranjan Uma Naresh, Shaden Smith, Ammar Ahmad Awan, Conglong Li, Yuxiong He (team lead)。
参考链接:
https://www.microsoft.com/en-us/research/blog/deepspeed-extreme-scale-model-training-for-everyone/
https://zhuanlan.zhihu.com/p/343570325
编译器并非是绝对智能的,也会存在很多 corner case,可以称之为优化盲区,而在了解一些编译器的操作之后,是可以提前预判到编译器的行为的,那么我们就能写出效果更好的代码。偶尔能看到一些编译器无法进行优化的案例,每次就默默地收集了起来。
内容来源:In C++, is empty() faster than comparing the size with zero?
在对链表进行 empty() 判断可以有如下的写法:
struct node {
struct node *next;
int payload;
};
int count_nodes(const node* p) {
int size = 0;
while (p) {
p = p->next;
size++;
}
return size;
}
bool is_not_empty(const node* p) {
return count_nodes(p) > 0;
}
在 GCC 进行 -O3 优化时,会发现 empty() 会变成 O(1) 的复杂度,而 clang 还是老老实实地跑循环 O(n):示例
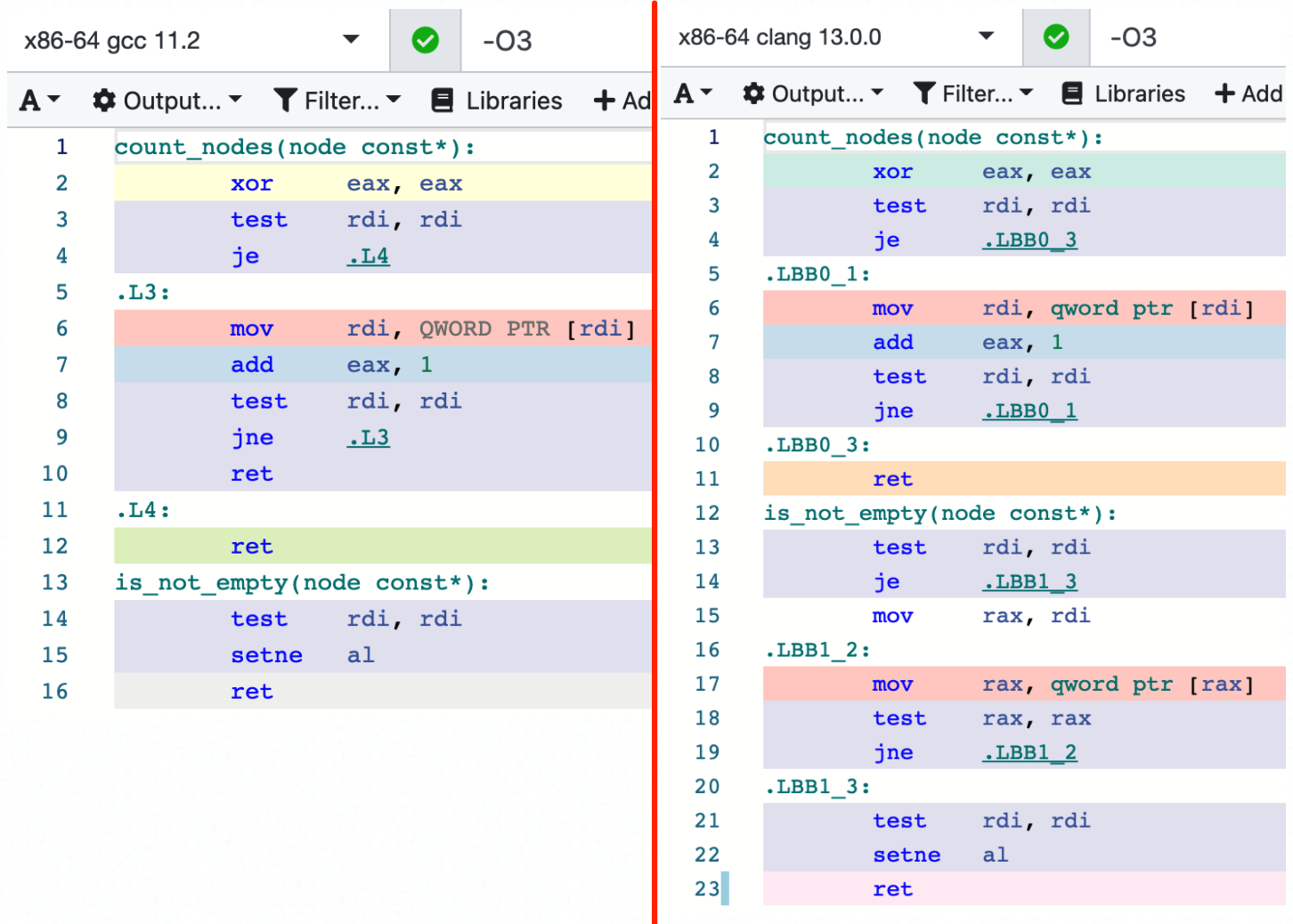
GCC 只用 test 指令判断指针不为空(NULL,0),就可以认为不是 empty 的。
而 clang 是 1、如果为空,再做一次判空,完成;2、如果不为空,跑个循环直到为空,再次判断第一个元素是否为空,完成。(你可能觉得 clang 多此一举,但编译器会考虑很多 corner case,所以还不够智能)
但如果把 count 函数改成无符号类型的话,GCC 也会变得无能为力:示例
size_t count_nodes(const node* p) {
size_t size = 0;
while (p) {
p = p->next;
size++;
if(size == 1000) {
return 1000;
}
}
return size;
}
该文作者给出的解释是,在有符号的情况下,编译器可以很好地判断不会发生 overflow。而在无符号的情况下,编译器还要处理 overflow 的情况,很难确认 count 函数会不会返回 0,所以作者在上述代码还给它加了个 1000 的数量限制,但遗憾的是,编译器还是无法对此进行优化。
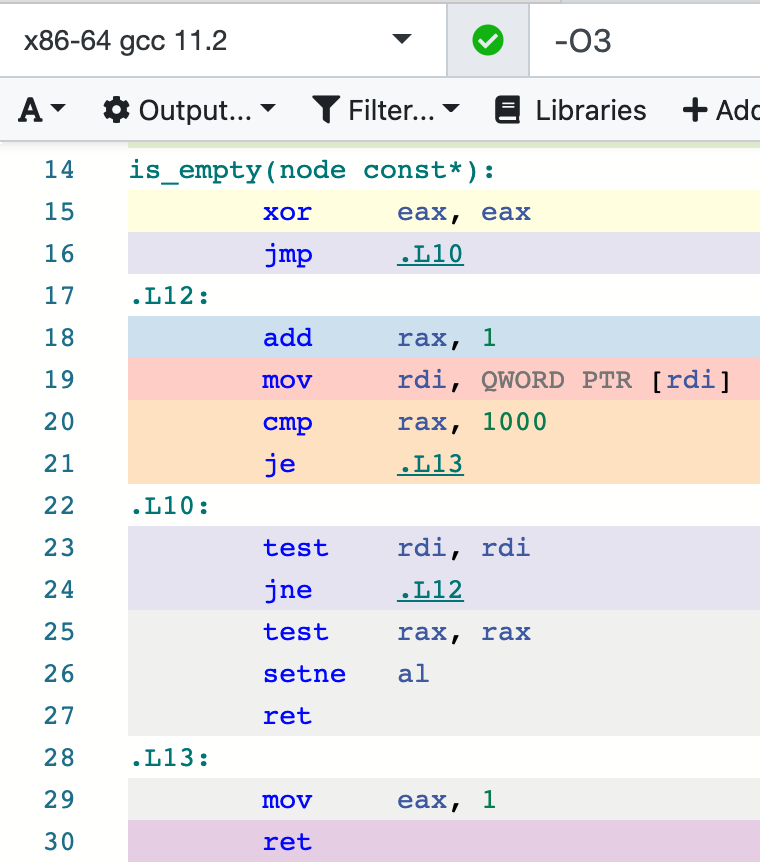
在一份 GCC 的资料里,我找到了相关的解释,这相当于是 GCC 对于优化的一个设定(GCC 假设有符号不会溢出):
-Wstrict-overflow=n
This option is only active when -fstrict-overflow is active. It warns about cases where the compiler optimizes based on the assumption that signed overflow does not occur. Note that it does not warn about all cases where the code might overflow: it only warns about cases where the compiler implements some optimization. Thus this warning depends on the optimization level.
内容来源:operator+ vs string append
const string GREETING = "hello ";
const string USER = "for testing the c++ string concat performance";
// 方案1
string concat = GREETING + " " + USER;
// 方案2
string concat;
concat.reserve(GREETING.size() + 1 + USER.size());
concat.append(GREETING);
concat.append(" ");
concat.append(USER);
上面这两个方案都是在做字符串的连接,但方案 2 是提前计算好字符串所需预留的大小,再进行操作。
直觉上是操作越少的越快,但是结论反而是方案 2 的性能更优,因为预留足够的空间来做字符串连接也是一项重要优化,而 clang 还没智能到直接算好需要预留的空间。
stack overflow 还有相关问题讨论:Most optimized way of concatenation in strings
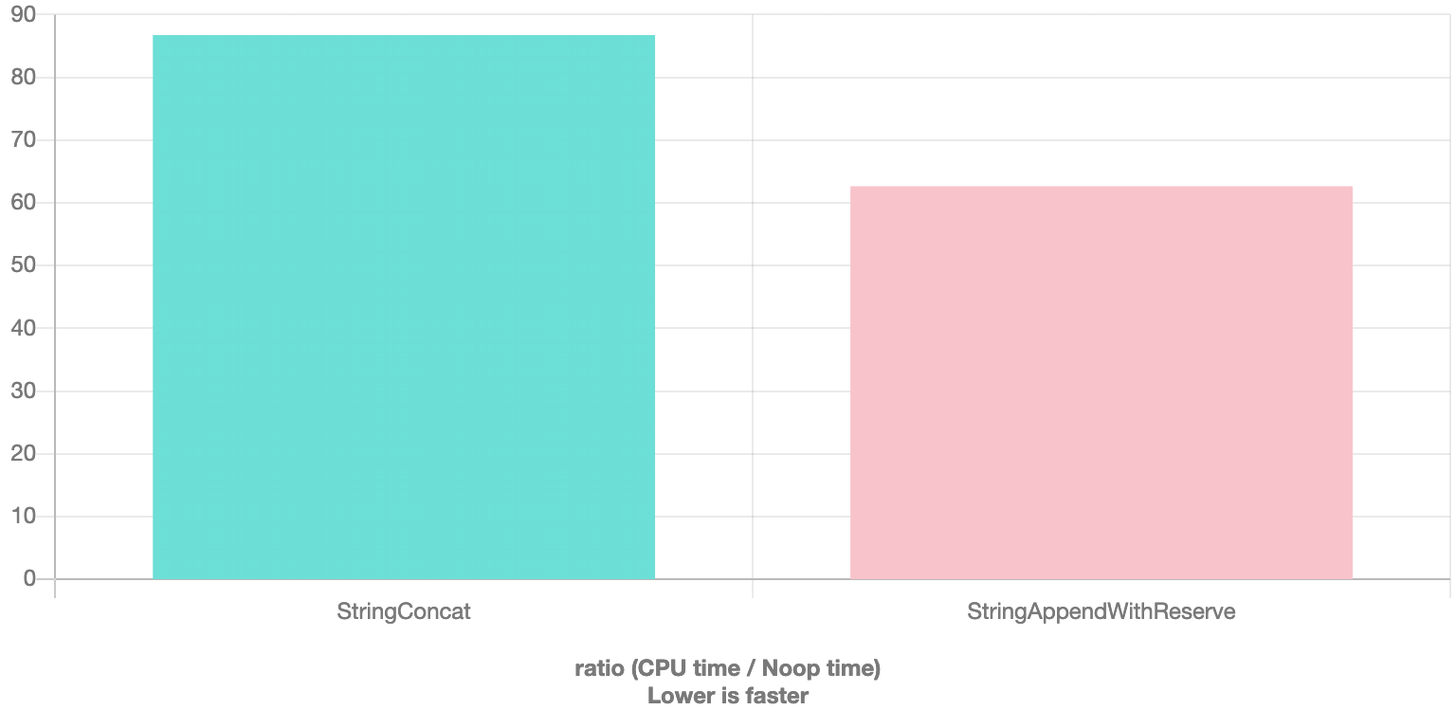
但是注意,对于合并总长度较短的字符串,先使用 reserve 可能会劣化,因为 std::string 对短字符串有做优化(Small Object Optimization,不另外开辟内存,直接在原有变量内存上存储短字符串)。
内容来源:https://travisdowns.github.io/blog/2019/08/26/vector-inc.html
对数组的每一个元素进行加 1 操作,下面有 uint8_t 和 uint32_t 两个版本,哪个会更快?
void vector8_inc(std::vector<uint8_t>& v) {
for (size_t i = 0; i < v.size(); i++) {
v[i]++;
}
}
void vector32_inc(std::vector<uint32_t>& v) {
for (size_t i = 0; i < v.size(); i++) {
v[i]++;
}
}
假设有接近 20000 个元素,直觉上是 8-bit 版本的会更快,因为占用的内存更小,同时也更能够满足 L1 cache,而且说不定还用上 auto-vectorization (自动向量化计算,如利用 SIMD(single instruction multiple data) 单条指令同时操作多个数据),那么 8-bit 版本应该更有优势。
但事实并非如此(数字越小,代表耗时越短):
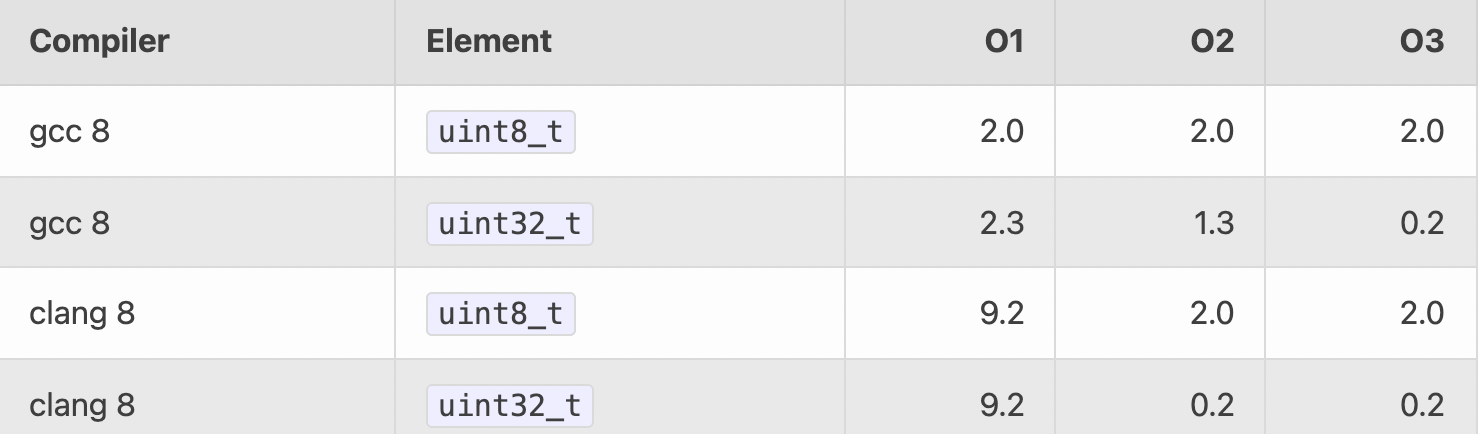
反直觉的,32-bit 的版本性能更高。
在 -O2 优化下,看看指令的差别:
; 8-bit:
.L3:
inc BYTE PTR[rdx+rax]; increment memory at v[i]
mov rdx, QWORD PTR[rdi]; load v.begin
inc rax ; i++
mov rcx, QWORD PTR[rdi+8]; load v.end
sub rcx, rdx ; end - start (i.e., vector.size())
cmp rax, rcx ; i < size()
jb .L3 ; next itr if i < size()
; 32-bit:
.L9:
inc DWORD PTR[rax]; increment memory at v[i]
add rax, 4 ; i++
cmp rax, rdx ; i < size()
jne .L9 ; next itr if i < size()32-bit 版本的循环体,少了对 vector::begin 和 vector::end 的加载、用 end - start 计算出 size。而 8-bit 把这些都放在循环体内,属于重复操作。为什么会产生这样的差异,原因就在于指针别名(pointer aliasing),下面会进行解释。
-O3 优化又做了什么,来取得了进一步的优化?
.LBB1_6:
vmovdqu ymm1, ymmword ptr[rax + 4*rdi]
vmovdqu ymm2, ymmword ptr[rax + 4*rdi + 32]
vmovdqu ymm3, ymmword ptr[rax + 4*rdi + 64]
vmovdqu ymm4, ymmword ptr[rax + 4*rdi + 96]
vpsubd ymm1, ymm1, ymm0
vpsubd ymm2, ymm2, ymm0
vpsubd ymm3, ymm3, ymm0
vpsubd ymm4, ymm4, ymm0
vmovdqu ymmword ptr[rax + 4*rdi], ymm1
vmovdqu ymmword ptr[rax + 4*rdi + 32], ymm2
vmovdqu ymmword ptr[rax + 4*rdi + 64], ymm3
vmovdqu ymmword ptr[rax + 4*rdi + 96], ymm4
vmovdqu ymm1, ymmword ptr[rax + 4*rdi + 128]
vmovdqu ymm2, ymmword ptr[rax + 4*rdi + 160]
vmovdqu ymm3, ymmword ptr[rax + 4*rdi + 192]
vmovdqu ymm4, ymmword ptr[rax + 4*rdi + 224]
vpsubd ymm1, ymm1, ymm0
vpsubd ymm2, ymm2, ymm0
vpsubd ymm3, ymm3, ymm0
vpsubd ymm4, ymm4, ymm0
vmovdqu ymmword ptr[rax + 4*rdi + 128], ymm1
vmovdqu ymmword ptr[rax + 4*rdi + 160], ymm2
vmovdqu ymmword ptr[rax + 4*rdi + 192], ymm3
vmovdqu ymmword ptr[rax + 4*rdi + 224], ymm4
add rdi, 64
add rsi, 2
jne .LBB1_6答案就是 auto-vectorization,整个循环体被向量化,可以在 L1 cache 中一次循环同时操作 8 个数据(256 bit)。
那么导致 8-bit 版本无法进行这些优化的罪魁祸首,就是指针别名了。
void vector8_inc(std::vector<uint8_t>& v) {
for (size_t i = 0; i < v.size(); i++) {
v[i]++;
}
}
首先数组 v 是通过引用而来的,实际上就是一个指针,编译器需要通过 v::begin 和 v::end 来计算出数组的大小 size()。
编译器需要在循环体中,一直获取 size(),因为它无法保证 size() 会不会在过程中被修改。
为什么呢?因为 v[i]++ 在写入未知的内存位置,编译器无法确认修改的会不会是 size() 的值。
那为什么只在 8-bit 版本上无法确认?因为对于大多数编译器而言:
uint8_t是unsigned char的别名(typedef)
unsigned char(或 char) 数组可以指向(alias,别名)任何类型
- 通过
uint8_t指针修改,会被认为有可能更新任意位置的内存
- 编译器认为
v[i]++会威胁到size(),所以每次循环重复计算
编译器有时候就是不够智能!
那么解决方法,就是让编译器认为我们不会在过程中修改 size() 的值。
for (auto i = v.begin(); i != v.end(); ++i) {
(*i)++;
}
在这里不再使用 size() 来做判断,而是使用 end() 来判断结束,编译器会优化成:
.L17:
add BYTE PTR[rax], 1 ; increment memory at *i
add rax, 1 ; next element ++i
cmp QWORD PTR[rdi+8], rax ; i !=v.end(),rdi+8 为 end 位置
jne .L17为什么要把 v[i]++ 改成 (*i)++ 了?因为 v[i]++ 可能会被认为是 *(v.data() + i),导致多出一次对内存的访问操作。
但这里还是会有冗余,对 end 内存访问的操作,那么提前计算好,就是给编译器最好的提示:
for (auto i = v.begin(), e = v.end(); i != e; ++i) {
(*i)++;
}
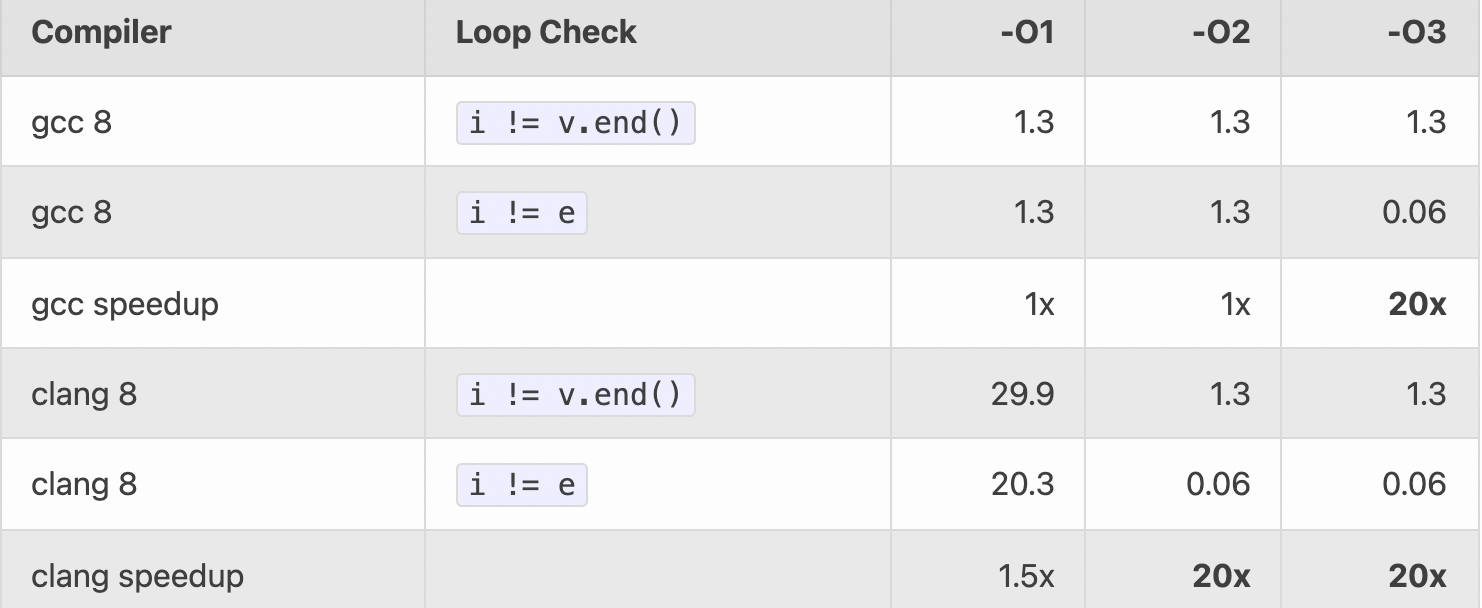
参考
In C++, is empty() faster than comparing the size with zero?
The point of test %eax %eax[duplicate]
Options to Request or Suppress Warnings
Most optimized way of concatenation in strings
本篇论文为Pure Tensor Program Rewriting via Access Patterns, 这是一篇基于EGraph对Tensor级别的IR进行Term Rewriting的从而自动发现卷积到im2col转换的文章.
对于现存的Pure IR比如relay等, 并不会关注底层的data layout 相关信息.另一边用于底层优化的IR却并不是Pure IR,难以进行term rewriting.为了解决这个问题,作者提出了Glenside(Access Pattern),一种Pure IR可以抽象出low level的硬件表示,同时经过term rewriting后甚至能自动发现im2col这种等效计算方法.
TVM 和 Halide已经通过简单的rewrite system做到了simplify和边界分析,但是现存的IR对于Tensor IR抽象和粒度不匹配还是影响了term rewriting,以上两个项目中都需要写出非常详细的pattern来进行 simplify的.
term rewriting面对的主要问题就是有副作用的IR, 因此需要提出一种没有副作用的IR, 同样也能表示这种操作. 传统的tensor通常用一个正整数tuple作为shape来表示的. 而Access Pattern替换了传统的表示方法, 使用两个shape来表示, 形如 ,通过这种表示方法将
tensor的迭代维度从计算的维度中分离开来.
比如一个三维的Tensor运算,典型如带有Batch的矩阵乘,在Batch维度进行迭代,在后面两个维度进行计算,其access pattern的示意图如下:
接下来我们尝试用Pure的IR描述一个矩阵乘, 首先用[A]表示一个由A类型组成的向量. 那么自然两个向量的内积表示为, 接着
2D Tanspose将表示为. 这里的
[[]]表示一个向量内部由向量组成,即代表2D矩阵.
我们知道2D的矩阵乘是计算输出 上每对
的行和
的列长度为
的向量内积, 其公式如下:
要进行计算,我们还需要引入map操作:
其中 是一个函数签名,他表示此函数将把类型A转换为类型B.
接下来定义一些计算函数如笛卡尔积:
关于笛卡尔积的计算流程, 我们假设这里的 和
都是一维向量
[f64],这里 就是表示的是
[[f64]],其中里面的维度是2, 外面维度和 相同, 最后外面再加一个维度得到
.
然后我们写出一个矩阵乘的表示:
其含义是 取出 的行和
的列组成数据对,然后每个数据对都应用内积求结果.
下面我简单的用代码描述了上述过程, 将matMul的表示实例化.此时我们需要注意到输出的数据类型就变成了[f64]. 各位读者也可以自己将P=[[f64]]带入上面的表示中自行推导一下.
import numpy as np
def dotProd(AB):
(A, B) = AB
assert A.ndim == 1
return np.dot(A, B)
def cartProd(A: np.ndarray, B: np.ndarray):
AB = []
for a in A.reshape((-1, A.shape[-1])):
for b in B.reshape((-1, A.shape[-1])):
AB.append((a, b))
return AB
def trans2(A: np.ndarray):
assert A.ndim == 2
return A.transpose()
def test_cardproduct():
P = np.random.rand(3, 4)
Q = np.random.rand(4, 5)
print(list(map(dotProd, cartProd(P, trans2(Q)))))
[0.10732114230108192,
0.21243371438870884,
0.34685428666259904,
0.14556577914149274,
0.23254688326914144,
0.5821735344411842,
0.9735256103240557,
1.9118977760582447,
0.5735451588389484,
0.5549736743719554,
0.31553182873079905,
0.582579830538644,
1.1357542180343412,
0.20513303615713718,
0.3916623321089719]那么问题就出现了,实际上我们的2D矩阵乘就是要得到2D的结果,而之前的表示得到的结果为[f64],很明显问题出在cartProd会将shape给展开, 因此简单的修改方法则是添加一个新的函数,来专门处理二维数组的情况:
但也不能直接用cartProd2D代替cartProd, 因为map时就会出错,不能把一个[[f64]]的输入传递给dotProd进行计算. 因此再添加一个新的mapAt2, 为map指定对应的作用维度:
那么经过修改后,目前的公式如下:
对应的代码实现如下:
def cartProd2(A: np.ndarray, B: np.ndarray):
n, m = len(A), len(B)
AB = [[1 for j in range(m)] for i in range(n)]
for i in range(n):
for j in range(m):
AB[i][j] = (A[i], B[j])
return AB
def mapAt2(func, A: list[list[any]]):
n, m = len(A), len(A[0])
B = [[1 for j in range(m)] for i in range(n)]
for i in range(n):
for j in range(m):
B[i][j] = func(A[i][j])
return B
P = np.random.rand(3, 4)
Q = np.random.rand(4, 5)
print(np.array(mapAt2(dotProd, cartProd2(P, trans2(Q)))))
[[1.90265933 1.37014723 1.90525837 2.16506508 0.8182536 ]
[1.74624439 1.06923152 1.74345372 1.85747233 0.82131666]
[1.88350644 1.49704492 1.93444511 2.1764349 0.8319122 ]]根据前文所提出的表示方法其实可以写出一系列的rewrite规则进行term rewriting了. 但是就像刚才我们需要添加cartProduct2D来适应更高阶的维度计算,当有个规则时依赖于特定维度的shape,我们首先得实现对应的算子,还得在所有的规则上添加新的规则转换,比如1D转换2D,2D转3D,将会出现组合爆炸的问题导致无法解决.
一种解决方法是添加lambda函数,通过偏函数的方式解决shape align的问题:
第二种解决方法使用index标记的方式:
但是上面两种方法实际上都是要添加name binding的,对term rewriting来说是很困难的,因为做rewrite的时候需要分析每个表达式上下文,当前的var bind到的是什么.作者利用egg尝试了实现,但是发现潜在的搜索空间膨胀问题还是难以解决.
以上遇到的问题就是Glenside需要解决的,即提供一个灵活的IR支持高阶的tensor的操作的同时支持高性能的term rewriting.
接下来主要介绍Access Pattern、 Access Pattern Transformer 、Access Pattern Operator三方面来讲明 Glenside的本质.
access pattern是一种通用的tensor IR描述表示形式, 他具体的将tensor的dimension分成了iterated over 和 computed on两部分. 其中iterated over表示的就是accessed,即计算入口位置 (这种思路和numpy的universal functions比较类似). 比如之前的matMul的例子,就是在dim 0进行迭代,在dim 1 进行计算.
access pattern 的具体写法是将tensor shape分为两个tuple组成的 pair,形如 ,那么
tensor 的shape 等于当前access pattern concat起来的结果. 给定tensor T, 我们用 表示
的长度, 此时我们利用语法
可以返回这个
tensor的access pattern, 比如 那么
就表示
的
access pattern.
access pattern transformer即转换一个access pattern生成一个新的access pattern, Glenside通过这种方式可以支持复杂的张量操作如slice/transpose. 其实就是作者发现一些tensor的operator的本质就是对数据访问改变了,因此修改access pattern正符合这个本质. 例如transpose操作, 从数据访问的角度就是先行后列变成了先列后行; 对于pad操作, 就是多访问了一些额外的元素. 那么用于描述访问的access pattern可以简单的表示这些操作.
同时access pattern的好处是他原生体现了tensor的shape信息, 我们无需像TVM/MLIR一样定义一套shape infer的图(如果是非常量的shape也可以用Glenside表示,后续可以做常量折叠等).
下面举个 : 比如我们要取张量 的每一列进行矩阵乘, 假设
的
shape为 ,
表示读取每一行进行计算
, 此时使用
transpose transformer 就表示把读取每一行的访问模式变成了读取每一列进行计算即:
接下来定义cartProd transformer如下:
其中 表示的就是
concat起来的两个子tensor.
在矩阵乘中, , 读取
的行与
的列
,然后带入
cartProd transformer得到 , 此时恰好表示在
的行与
的列上每次取两个长度为
的向量.
operator是Glenside中表示计算的IR. 他们只在添加compute前缀时才被invoke(区别于access pattern transformer), 即把操作映射到access pattern的compute维度上, 最终返回的access pattern中compute维度会被修改为operator函数签名所指示的.
将上一节通过cartProd之后得到的
access pattern应用compute dotProd之后的得到了 , 最后一个矩阵乘的
Glenside形式如下:
接下来主要是展示Glenside将典型的一些深度学习kernel如何自动映射到加速器上.
- 2D Convolution
卷积的计算公式如下:
转换为Glenside表示:
首先取出weights的 ,然后使用
windows的操作生成新的access pattern , 即对于输出的每一个的像素位置,取一个原始的输入窗口, 而后每个窗口和卷积的
filter 进行外积后计算内积, 最后用squeeze和transpose得到输出的结果.
- Max Pooling
其数学公式如下:
他的Glenside表示与卷积类似,windows之后reduce即可:
我觉得Glenside把访问和计算分离的方式就极大的简化了计算的算子, 因为访问变换的时候其实包含了传统表述中计算的一部分.比如上面的两个例子中, conv2d和maxpool的核心都是取window然后计算,一个是取3d一个取2d, 但是此时取window的并不是在window函数上配参数,而是直接把这个信息附加到tensor自身上了. 这种表示方法虽然无法和通常的数学计算流程表示一一对应,但是他作为IR就起到了很好的桥梁作用,并且他这个内积外积设计就和很多加速器的核心逻辑一致.
Glenside所提出的demo是一个weight-stationary的脉动阵列,然后Glenside基于egg的库添加了一系列的规则,下面是将矩阵乘转换为脉动整列计算的规则:
脉动阵列的形状参数由 和
所决定,同时在接下来的
access pattern中更加细致的表示硬件如何访问tensor,首先是读取所有的数据 ,然后在内存中进行
transpose.这种更加细致的表示方法可以提供更加丰富的数据layout信息,对于后续的优化/codegen有潜在的好处.
im2col的布局转换可以提升计算速度,虽然会导致一部分的内存开销. 这种transform涉及直接在内存中对windows操作实例化,虽然会导致额外的数据复制,但是只要这个开销小于取偏移的开销就是有好处的. 接下来Glenside将展示如何自动发现im2col的transform.
首先上面提出的脉动整列转换都是只针对单纯两个向量计算的映射,而卷积/矩阵乘最大的问题就是最后的内积/外积操作输入的tensor维度并不确定,所以需要先自动的把access pattern的维度降下来转换到脉动阵列上,不然我们又回到了为每个场景写pass的情况了.
Glenside提出了exploratory rewrite, 即添加一系列看似无效的操作从而引入潜在的rewrite机会.比如把一个access pattern展平之后并reshape为原样,这样就能解决之前规则中维度不匹配的问题.
不过这样也带来了一个问题,添加了reshape之后还需要消除它才能真正的进行脉动阵列的转换,因此又添加了关于reshape与cartProd/dotProd计算的composition commutativity规则,将reshape操作从表达式中移除(意思就是这里直接手动加两个规则规避一下比较简单).
最终的结果证明了只需要寥寥几个规则就可以达到传统手写pass的程度,编写的复杂度更低,同时无需考虑pass ordering的问题.
接下来作者探索了用Glenside做tiling,比如把 转换为多个
小矩阵乘. 和脉动阵列一样,作者也是需要一个探索性的rewrite以及一些消除多余operate的
rewrite,这里的探索性rewrite那肯定就是slice/concat了:
不过这个探索性太强了,如果全部都组合肯定直接爆炸,因此作者设置的每次切一半,保证是2的倍数.然后再添加一些规则消除计算前的concat/slice.
Glenside有效的解决了底层IR与DSA的映射问题.- 可以利用
egraph的特点去做到一些自动发现乘加矩阵融合等优化,可以帮助我们减少寻找等效操作的时间了, 不过有时候等效也并不一定完全等效, herbie这个项目就表明有时候形式一致但可能存在不同的数据溢出问题, 需要把这些都考虑进去能更好. - 作者提到
rewrite和polyhedral是可以结合起来的, 不知道有了Glenside做tiling能达到polyhedral多少效果.
看了 C++ 的虚函数的一些文章,对于其性能消耗的优化思路整理了一下。
对于虚函数,编译器可以通过关键字 virtual 识别,并为它们创建虚表,虚表保存着指向函数地址的信息。当一个具有虚函数的对象(object) 被创建时,编译器也会为它创建指向虚表的虚指针。
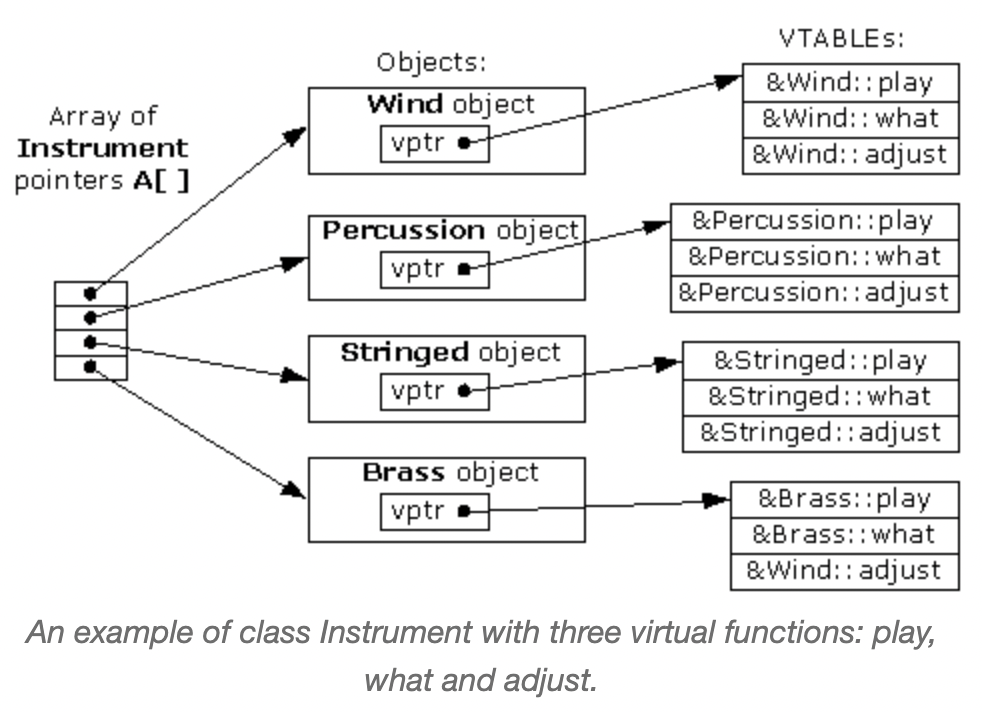
所以要访问到对应的虚函数,每次执行需要先解引用虚指针,偏移到虚表对应函数位置,然后调用。虚函数的开销主要体现在:
- 由于这个操作需要在运行时完成,所以虚函数没法像普通函数一样被 inline,同时也就失去了一些优化机会(inline 后可以进行更多的优化,如常量传播)。
- 现代 CPU 在进行分支跳转前会进行分支预测,对于虚函数而言,硬件在很晚的时机才会知晓要跳转的位置,这可能会导致存在分支预测失败的额外开销。
- 多次调用不同实现的相同符号的虚函数,对 cache 不友好。

根据性能测试结果,文章作者给出了以下建议:
- 合理安排对象的内存位置。带来更好的局部性。
- 尝试把一些小的函数脱虚(变成普通函数调用一样)。小函数的调用开销比执行更高。
- 把数组里的对象先按类型排好序。这样对 cache 会更友好。
-fstrict-vtable-pointers 是一个编译器参数,用来向编译器保证在对象的生命周期内,虚指针是固定不变的。这样编译器就不需要多次对虚指针解引用了,对于执行频率高的虚函数和分支预测可能都有一定的优化。
先看一个例子,在正常的虚函数调用下,每次虚函数调用之前,都会需要指令先解引用虚指针:
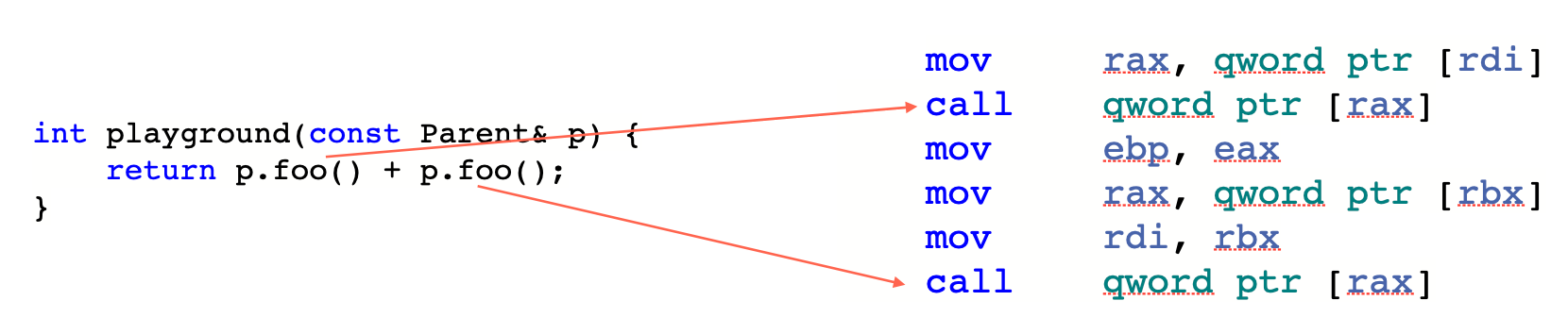
加上 -fstrict-vtable-pointers 后就不需要重复解引用虚指针了,因为我们向编译器保证了虚指针不会中途被改变。

multivector 是不同类型数组的集合,声明类型为 template <typename... Types> std::tuple<std::vector<Types>...>,按类型来划分到不同的容器中,实际上就是借助 template 来消除虚函数动态派发的操作,同时也更好地满足局部性。(点链接查看具体数据结构实现)
//实现
template <typename Function, typename T>
void for_all_p(Function fn) {
std::vector<T>& my_vector = get_vector<T>();
for (auto it = my_vector.begin(); it != my_vector.end(); ++it) {
fn(*it);
}
}
template <typename Function, typename T, typename Arg, typename... Args>
void for_all_p(Function fn) {
for_all_p<Function, T>(fn);
for_all_p<Function, Arg, Args...>(fn);
}
// 调用
jsl::multivector<circle, line, rectangle, monster> mv;
bitmap b(640, 480);
// Filling the container with random shapes
// ... ...
mv.for_all([&b](auto& o) { o.draw(b); });
还有把运行时多态改造成在编译期解析的方式,称之为 CRTP(Curiously Recurring Template Pattern)。如果模版看起来还理解吃力的话,可以用之前推荐过的工具 c++ insight 先解析一遍。
template <class T>
class Base {
public:
void Foo() { // 作为转发
static_cast<T*>(this)->FooImpl();
}
};
class Child1 : public Base<Child1> {
public:
void FooImpl() {
std::cout << "hello1" << std::endl;
}
};
class Child2 : public Base<Child2> {
public:
void FooImpl() {
std::cout << "hello2" << std::endl;
}
};
template <class T>
void Print(Base<T>& base) {
base.Foo();
}
来看个具体的函数调用的案例:
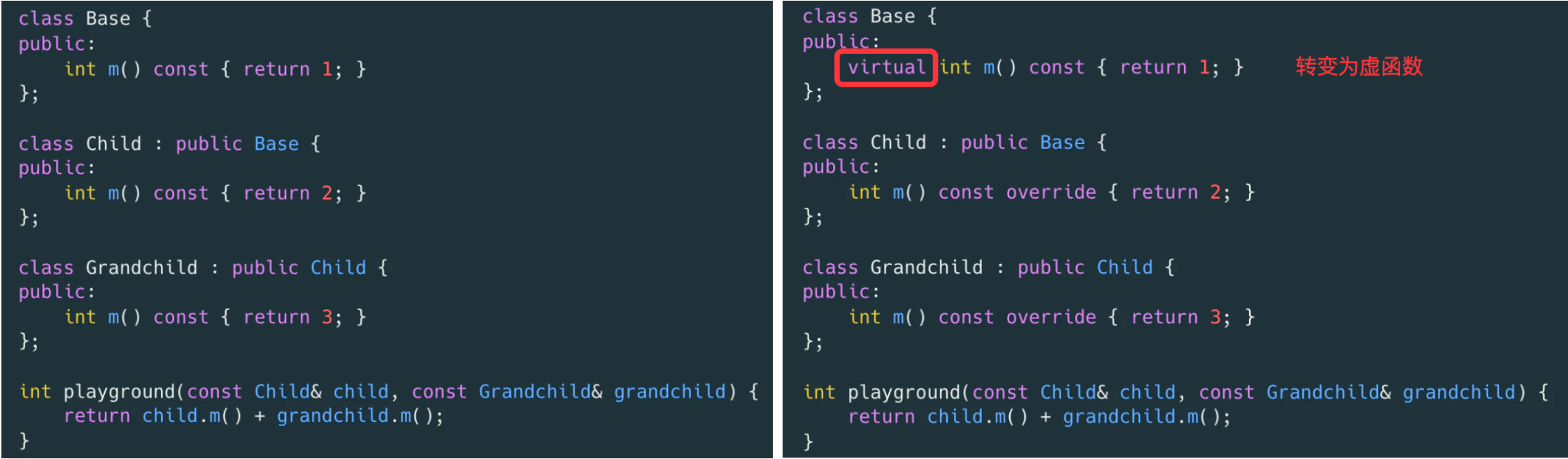
可以直接从它们的二进制指令看出区别:
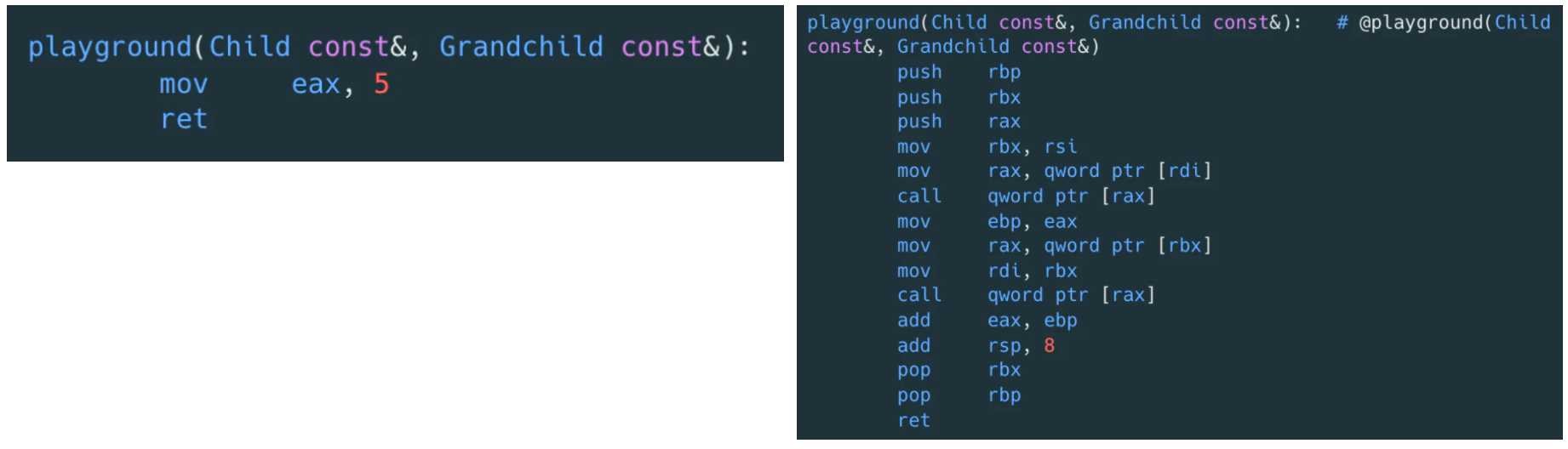
实际上对于 playground 函数的参数,在继承链上,如果我们确认 Grandchild 类型不会扩展子类,或者某个函数不会被重写了,则可以通过 final标记虚函数表示该函数不会有重写了。编译器就可以用直接函数调用来替代虚函数调用了,同时可能带来 inline 等优化。
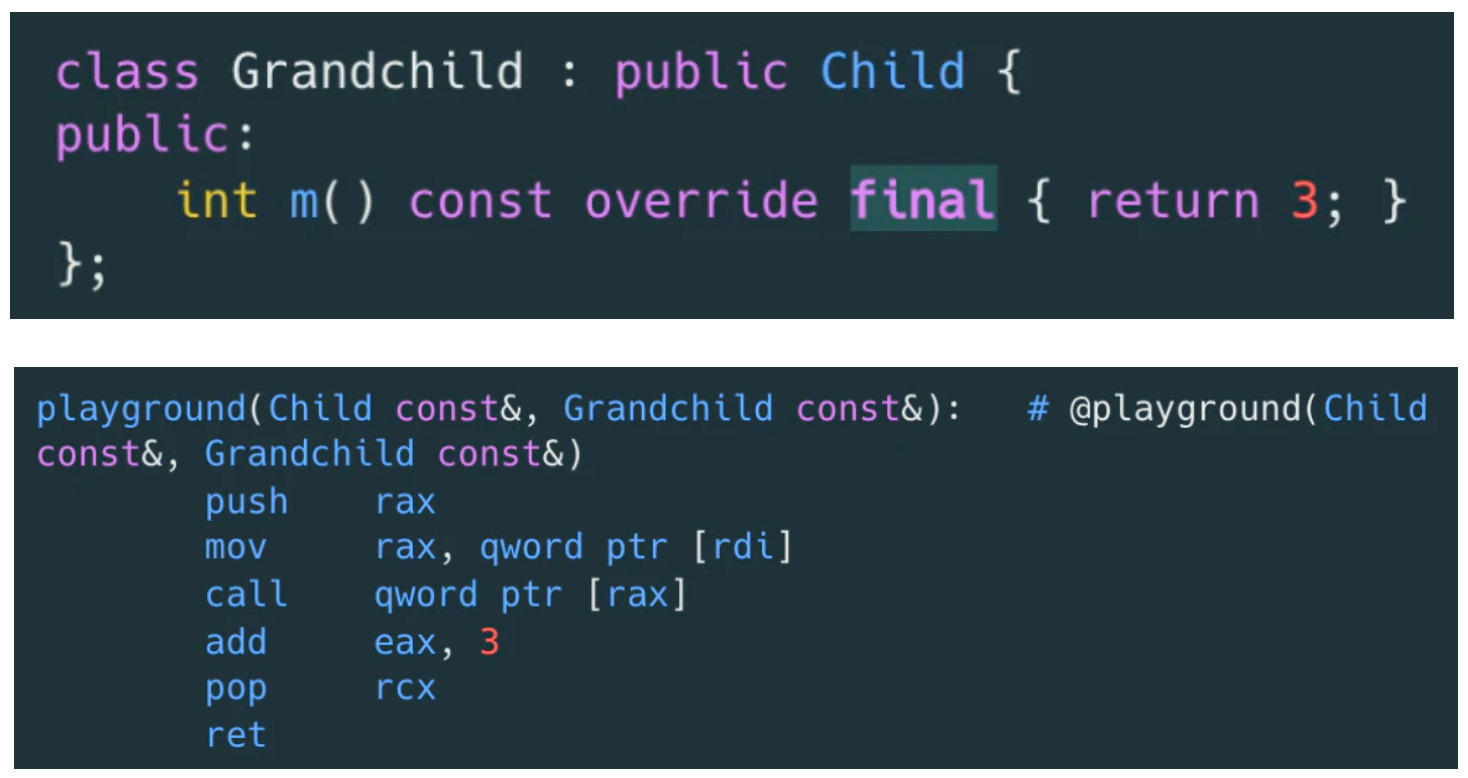
final 也可以用在对象上:


字节有篇文章也讲到这个的原理,有点像分支预测一样,把一个大概率调用的虚函数提前预测判断,是的话就直接调用,否则用指针间接调用(可以结合 PGO 的 profile 信息辅助判断)。
addr = vtable.do_something.addr@foo // 虚函数指针
if (addr == FooImpl::do_something) // 假设大概率为 FooImpl 对象
FooImpl::do_something() // 直接地址调用
else
call *addr // 指针间接调用
虽然增加了指令,但实际上只是一个地址比较的指令,而且直接调用可以被优化成 inline,有更多的后续优化机会,这里是优化了 indirect call 的消耗。但预测失败是可能导致负优化的,所以需要结合 PGO 的 profile 信息进行操作(Indirect Call Promotion)。
知晓全部的继承链图信息是关键,使用 LTO 是其中一种方式,在链接期同时也具备了链接信息(internal、external 等),可以做 devirtualization 的操作。

当一个类被定义在匿名命名空间,且在当前编译单元中没有子类,则可以把虚函数调用确切地改为对函数的直接调用。
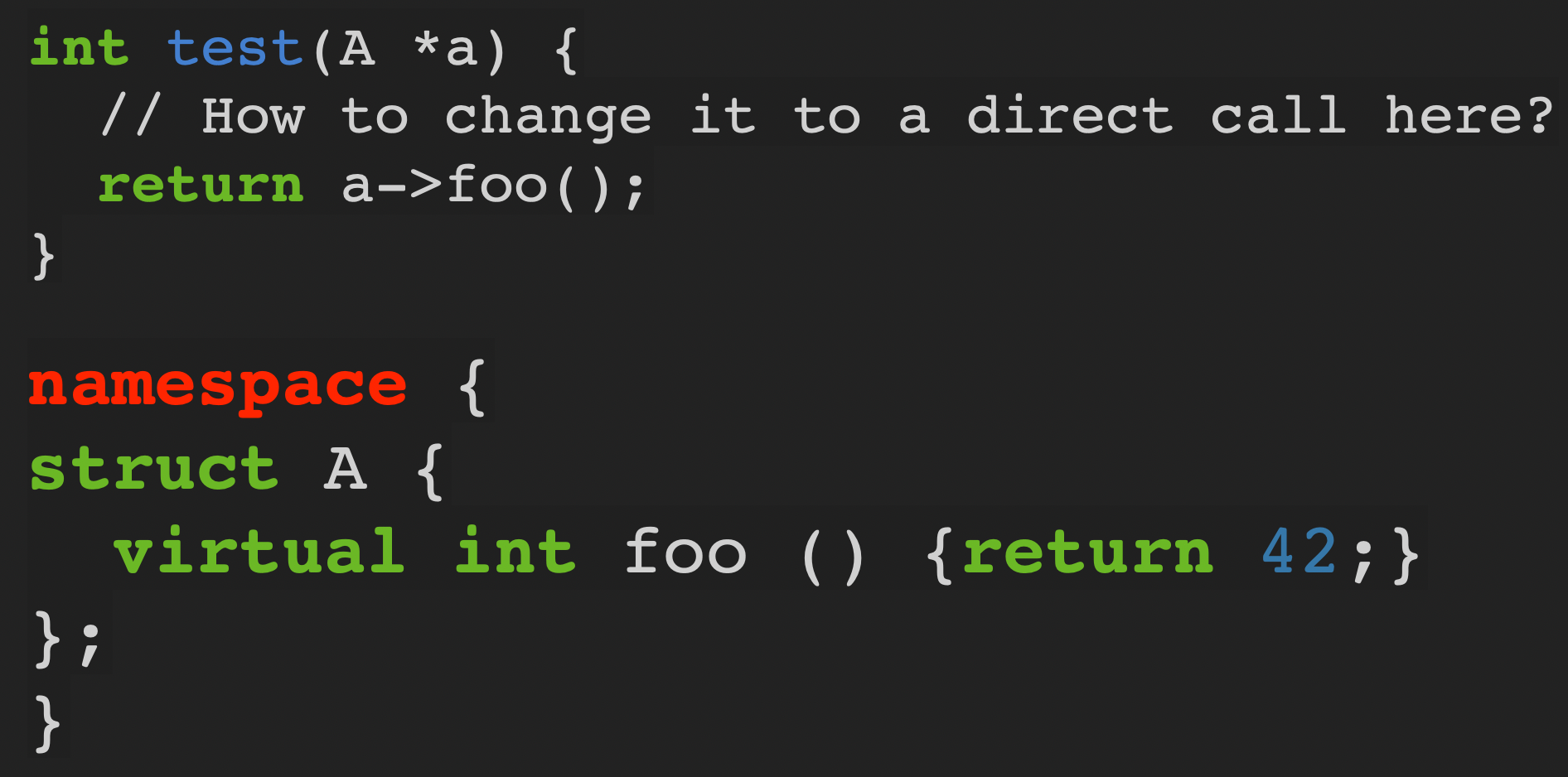
- The true price of virtual functions in C++
- 醒醒吧,静态多态根本没有这么香
- Add -fstrict-vtable-pointers to UserManual
- Virtual functions strike again.
- Final override
- 字节跳动 Service Mesh 数据面编译优化实践
- When can the C++ compiler devirtualize a call?
- Devirtualization in LLVM and Clang
- Profile-based Indirect Call Promotion
- DEVIRTUALIZATION IN LLVM
目前对于许多端侧NPU来说,是由一个可编程操作但容量较小的SRAM进行数据调度,需要尽可能的减少数据搬运, 从而避免DSA中的计算单元处于空闲状态[1]。
因此我们要解决的问题是:
- 如何充分利用
Local Memory并在减少读取Input的同时计算尽可能多的kernel? - 如何调度
Local Memory中的内存/指令从而充分利用计算单元?
本文主要分享关于Fused Layer内部的Buffer Schedule与Instruction Schedule的一些经验体会.
首先需要保证多个层之间的计算不回到DDR, 才能减少外部带宽, 充分利用Local Memory, 因此需要进行Layer Fusion:
- 需要实现高层IR的
Index Mapping进行Infer Bounds.[2] - 利用
DSL编写一系列的Tiled Tensor Operation实现.[3] - 将多层Kernel的DSL实现通过表达式的形式组织成
PrimFunction.[1] - 分析此
PrimFunction, 并进行Buffer Schedule与Instruction Schedule.
因为在编译的过程中需要尝试大量的Fusion Group以及各种Tile Size的组合, 因此没有将PrimFunction内部进行Unroll, 仅通过遍历PrimFunction内部Block对Buffer Usage/Lifeness进行分析, 添加Tiled Tensor Operation中所需要的各种约束信息, 然后求解2D Bin Packing问题.
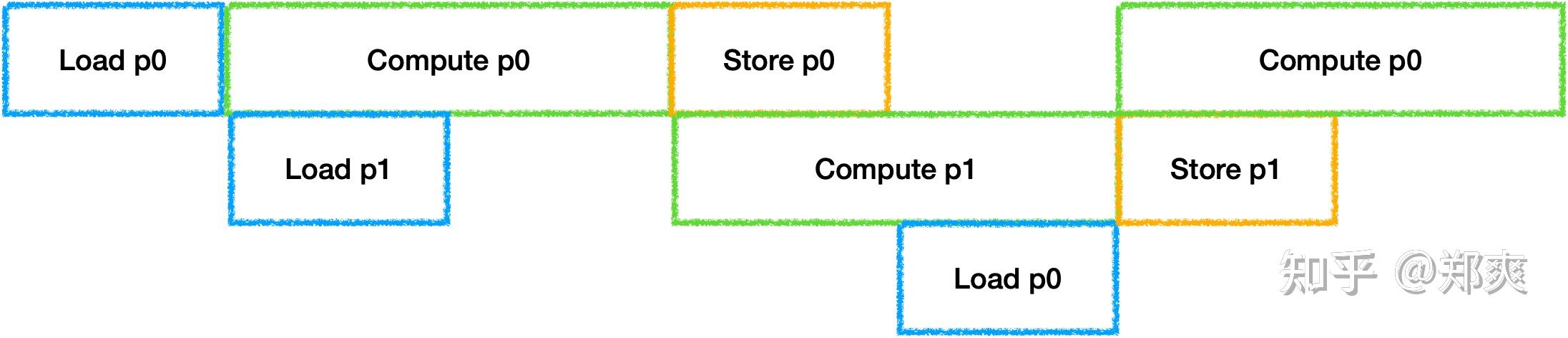
最简单的执行策略是将每个Tile中的Tensor Operation串行执行, 假设三个卷积的情况如下:

此时我们可以在计算上一个结果时加载下一个操作所需要的数据,但是通常对于神经网络来说,越后面的层Weights越大,在带宽与算力无法平衡的时候就会等待Load从而产生IDLE. 因此可以选择将Weights等参数长驻在Local Memory中,通过空间换时间(Trade-off项加一).
这里我选择将Weights等参数常驻后, 假设为6层卷积的Fusion进行无Bank Conflict的Buffer Schedule, 结果如下:
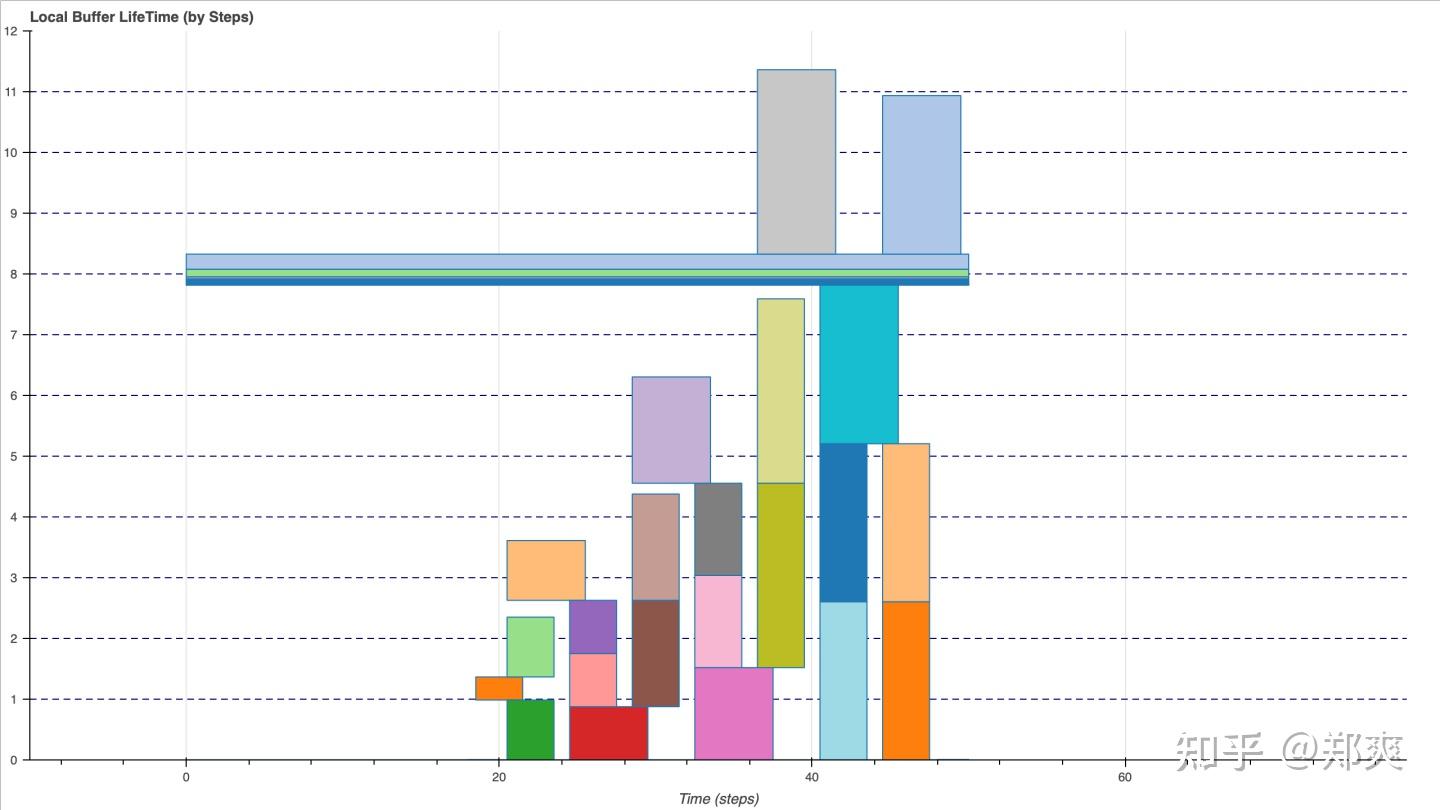
对于带宽受限的DSA来说, 虽然优化内部Buffer的布局可以更好的避免Bank Conflict从而提升计算效率,但是也会因为数据不连续导致Load/Store效率降低, 因此需要进行Trade-off.
为了充分利用器件, 每个Tile之间的IDLE也需要进行消除. 通常的做法是开辟并行器件数个Buffer来进行计算, 最理想的状态是每个器件的工作时间等长:
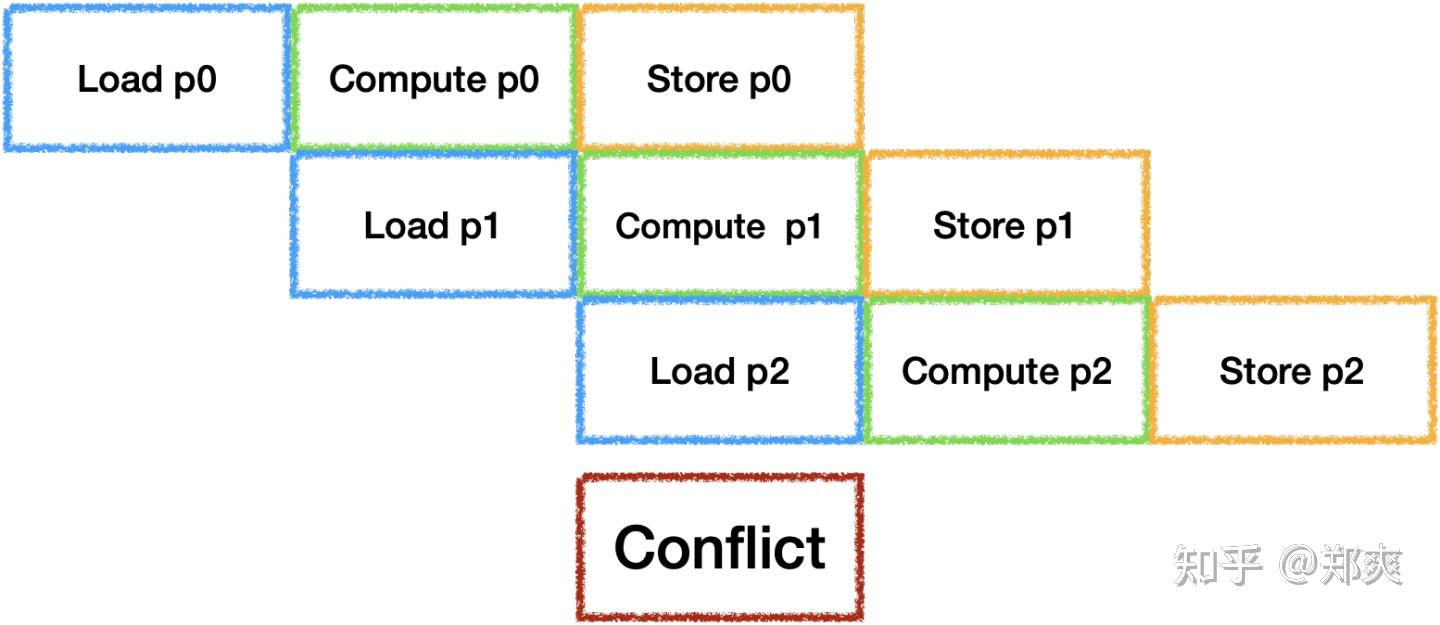
虽然Load/Store是可以并行工作的, 但是他们会抢占带宽资源, 此时还无法准确估计时间, 因此在带宽受限的场景下可以默认将他们视为同一个器件. 不过由于带宽受限, 在三器件并行双Buffer的情况下很还是容易出现每一对Ping Pong之间出现冲突与空闲:
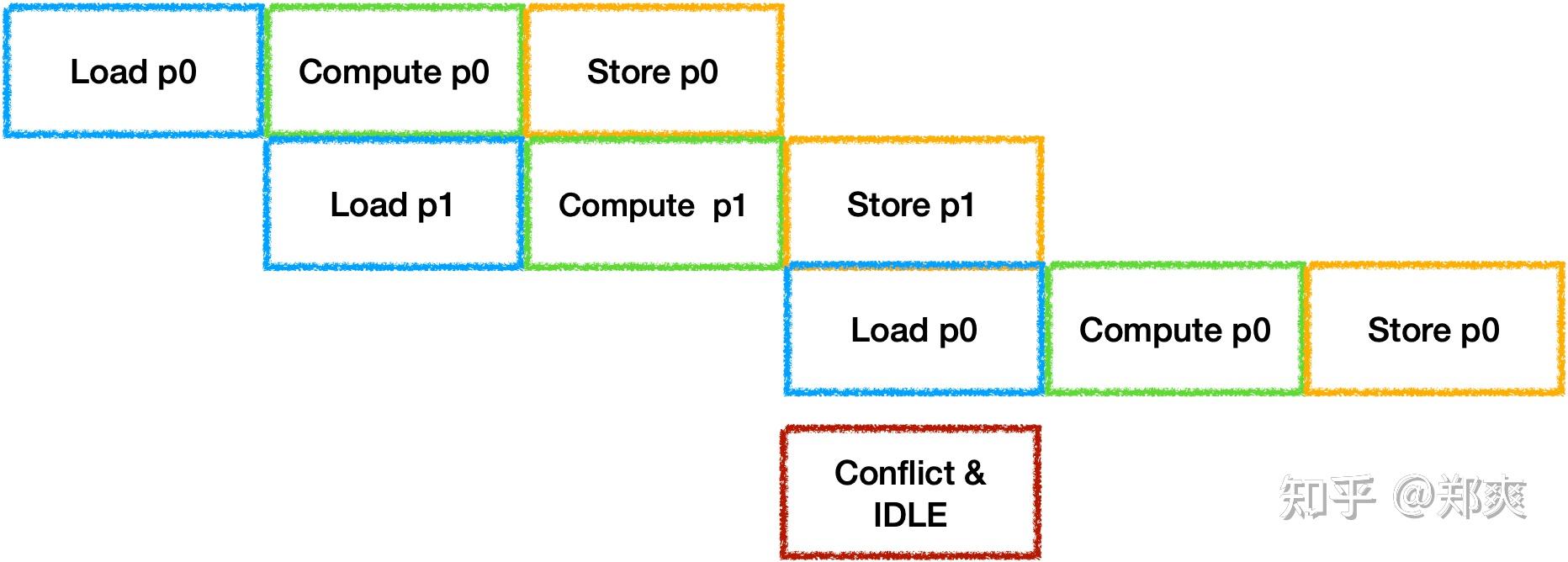
因此需要通过量化估计的硬件执行时间来选择Fuse足够多的层或切分足够的大小来保证Compute Time >=(Load Time + Store Time), 从而让计算器件连续工作.
如果当硬件中还有其他计算设备存在, 情况会更加多样, 假设再增加一个计算器件时(这里假设计算设备时间为3:7,同时总时间大于Load + Store):
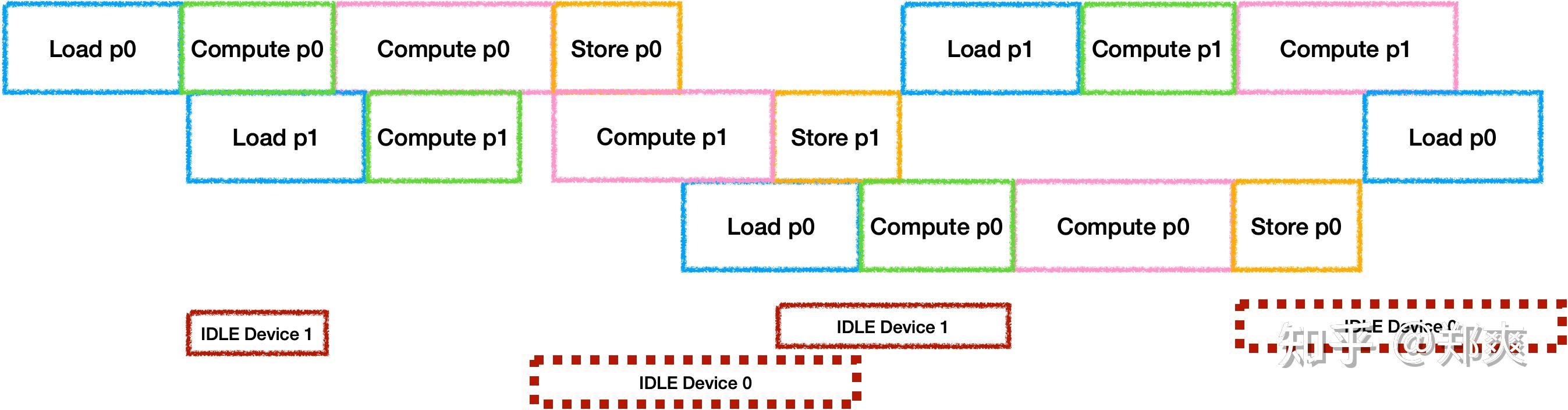
只开辟两个Buffer是会导致计算器件产生空闲, 他们空闲时间的比例与计算时间比例相同. 那么为了充分利用两个计算器件, 就需要再开辟新的Buffer, 此时只会因为计算时间不同导致其中一个计算设备出现空闲. 总之, 在有多个计算设备的情况下, 要量化增加Buffer数量带来的并行时间收益与随之增加的ReCompute进行Trade-off.

下面就是三块Buffer的实际分配情况, 可以发现为了减少Bank Conflict所造成的内存浪费是比想象中大的.

当多层Fuse之后, 生成的指令也会随之增多, 因此会遇到指令阻塞的情况, 比如当Compute的指令过多导致一下个循环中Load指令下发不及时的问题:
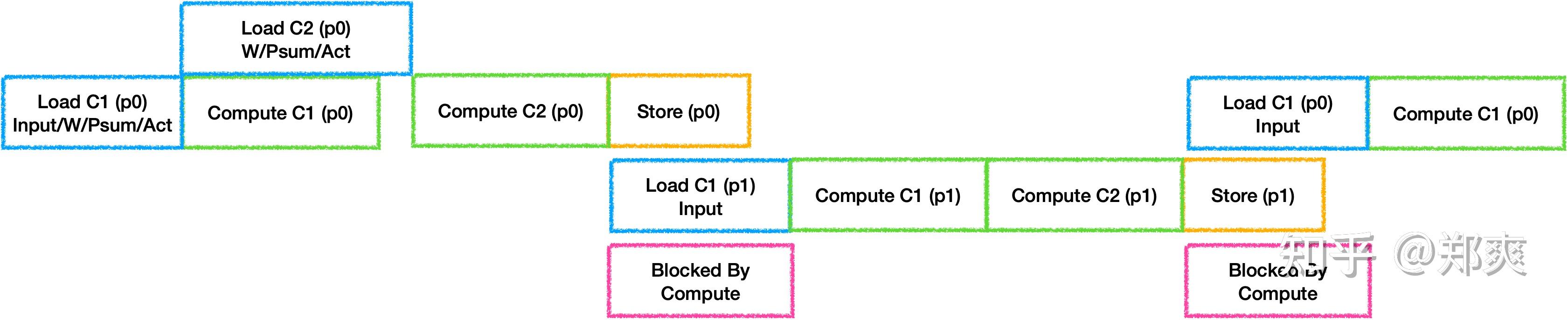
需要通过模拟指令队列来调整指令顺序, 实际上就是需要找到合适的Prefetch时机, 从而做到真正的流水.

Tile Size搜索策略问题
- 如果完全尝试所有的可能情况时间成本将会太高, 而按照程序既定的策略搜索又难以达到最优, 我个人认为是需要建立一种
Tile Size在各个维度上的变化对于执行时间(重计算/Load Store速率/器件流水)变化的联系来指导搜索, 可能需要借助一些机器学习方法.
多分枝结构Layer Fusion内部调度问题
- 当多分枝的结构在
Local Memory中执行时, 两个分枝没有依赖关系就需要再按拓扑排序进行调度, 找到峰值内存最小的执行顺序后再开始进行Tiling.
全局最优
- 需要如类似[4]的做法来尝试尽可能多的情况,来获得最优的
Fusion Group解. - 在尝试每个情况就需要在以下
Trade-off找到局部最优: - 是否选择重复
Load部分数据, 以时间换空间? - 是否优化数据布局, 牺牲
Load/Store效率提升计算效率? - 是否使用更多的
Buffer, 增加ReCompute换取更多并行? - 类似地平线编译器使用强化学习来进行优化可能是一个不错的选择.
以上内容仅代表个人观点,欢迎各位大佬指点交流.
Egg是一个基于EGraph的程序优化框架, 作者在其中实现基于Equality Saturation概念的优化方法, 简单来说就是通过将所有的表达式保存在EGraph这个数据结构中,可以按任意顺序实施RBO(基于规则的优化), 因为其中同时存储了所有可能的表达式, 所以没有传统优化中phase ordering的问题, 最终可通过CostModel提取出最优的图结构.
Egg在编译优化方面已经有许多应用了, 比如王润基大佬写的SQL 优化器, 其中也详细解释了Egg的使用, 不了解的朋友可以参考一下.
在端侧AI编译中,每个阶段都需要大量的优化与trade-off, 比如中端的计算图优化与后端的算子Fusion以及后端算子的量化类型(平衡精度/速度), 如果基于传统优化方式, 可能许多模型最优的Pass顺序,算子Fusion方案都需要编译器工程师手动调试与指定. 这主要就是因为传统优化方式一旦lower之后就丢失了之前的信息, 失去了最优的可能性, 因此考虑采用Equality Saturation技术来将中端优化/后端Fusion/Tiling/算子精度选择都放入其中进行整体性优化,希望可以得到尽量优化的编译结果.
不论是中端优化还是后端Fusion, 都会涉及到算子的折叠与合并. 通常无分支的算子的合并, 那么合并后Cost必然减小, 可以自然的选择当前Cost最小的表达式. 但是如果多分支的情况下就会遇到问题.
假设我们导入的模型有卷积/激活等算子,在Cpu上我们支持的Relu6/Clamp算子,他们的Cost分别为60,70. 后端支持卷积Conv,通用激活Act,以及卷积+通用激活ConvAct, 设他们的Cost分别为100,50,125. 其中执行ConvAct肯定是快于分别执行Conv和Act.
考虑如下的模型结构:

同时我们的存在这样一个Rule : rw!("fold_conv_act"; "(act (conv2d ?x))"=> "(conv2dAct ?x)"), 在经过Egg的Runner实施优化后, 得到了这样的结果:
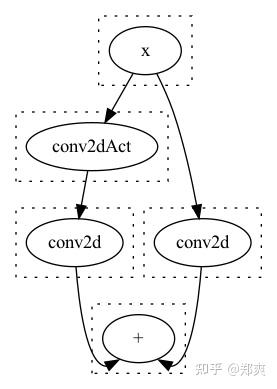
大家可以发现, 虽然我们合并了一个Act, 但是反而多计算了一次Conv, 最终的计算时间增加了.
Egraph中保存了展平的数据结构, 对于每一个Eclass选择其内部最小Cost的ENode来作为它的Cost. 但是因为EGraph中找不到入口点, 所以是反复遍历所有的EClass, 直到每个Eclass不再减小时退出.
其核心逻辑如下:
let mut did_something = true;
while did_something {
did_something = false;
for class in self.egraph.classes() {
let pass = self.make_pass(class);
match (self.costs.get(&class.id), pass) {
(None, Some(new)) => {
self.costs.insert(class.id, new);
did_something = true;
}
(Some(old), Some(new)) if new.0 < old.0 => {
self.costs.insert(class.id, new);
did_something = true;
}
_ => (),
}
}
}
.
.
.
fn make_pass(&mut self, eclass: &EClass<L, N::Data>) -> Option<(CF::Cost, L)> {
let (cost, node) = eclass
.iter()
.map(|n| (self.node_total_cost(n), n))
.min_by(|a, b| cmp(&a.0, &b.0))
.unwrap_or_else(|| panic!("Can't extract, eclass is empty:{:#?}", eclass));
cost.map(|c| (c, node.clone()))
}
问题就在于make_pass的时候他无法得到上下文的信息, 如下图所示:
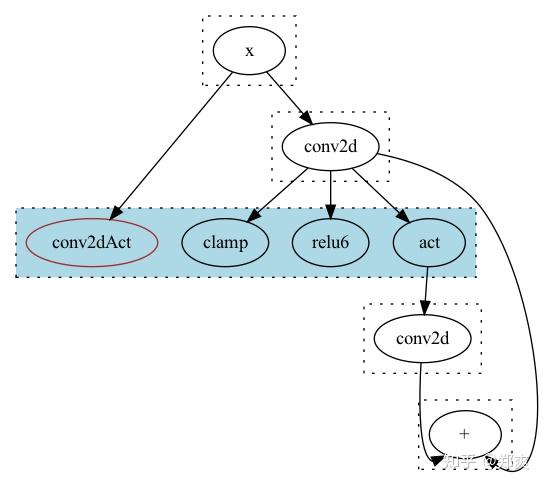
在蓝色的EClass中它自然会选择当前的conv2dAct节点,因为它是当前Eclass最小Cost的ENode.
下面写两个我思考的方案, 也欢迎大家在评论区一起讨论.
简单的方案可以在编写rule的时候判断要折叠的算子的user个数,如果是会引起这种现象的情况, 就不进行折叠. 不过这样总觉得和Equality Saturation的思路相悖, 不是一个很完美的做法.
需要记录每个ENode可能的Compute Sequence, 如同上图所展示的那样, 比如对于Add节点左边可能存在x -> conv2d -> relu6 -> conv2d, x -> conv2dAct -> conv2d等4种情况,右边则只有x -> conv2d一种情况, 然后消除两边计算序列的交集, 从而算得正确的cost值. 不过这样存储的Compute Sequence在每经过一个EClass时,都是按EClass.Nodes.Count来翻倍的, 需要一种节省内存的数据结构. 同时因为计算Cost的时候是将所有表达式展平之后处理的, 还需要方便的从中间节点进行替换. 总之不是一个容易实现的方案.
最小的复现代码NN.rs, 可以放在egg/tests目录下运行:
use egg::{rewrite as rw, *};
use ordered_float::NotNan;
pub type EGraph = egg::EGraph<NeuralNetwork, ()>;
pub type Rewrite = egg::Rewrite<NeuralNetwork, ()>;
pub type Constant = NotNan<f64>;
define_language! {
pub enum NeuralNetwork {
"+" = Add([Id; 2]),
"-" = Sub([Id; 2]),
"*" = Mul([Id; 2]),
"/" = Div([Id; 2]),
"conv2d" = Conv2D(Id),
"act" = Act(Id),
"relu6" = Relu6(Id),
"clamp" = Clamp(Id),
"conv2dAct" = Conv2DAct(Id),
Constant(Constant),
Symbol(Symbol),
}
}
pub struct CostFn<'a> {
pub egraph: &'a EGraph,
}
impl egg::CostFunction<NeuralNetwork> for CostFn<'_> {
type Cost = f32;
fn cost<C>(&mut self, enode: &NeuralNetwork, mut costs: C) -> Self::Cost
where
C: FnMut(Id) -> Self::Cost,
{
// let id=&self.egraph.lookup(enode.clone()).unwrap();
let mut costs = |i: &Id| costs(*i);
let op_cost = match enode {
NeuralNetwork::Conv2D(..) => 100.0,
NeuralNetwork::Act(..) => 50.0,
NeuralNetwork::Relu6(..) => 60.0,
NeuralNetwork::Clamp(..) => 70.0,
NeuralNetwork::Conv2DAct(..) => 125.0,
_ => 1.0,
};
let c = enode.fold(op_cost, |sum, id| sum + costs(&id));
c
}
}
#[rustfmt::skip]
pub fn rules() -> Vec<Rewrite> { vec![
rw!("fold_conv_act"; "(act (conv2d ?x))" => "(conv2dAct ?x)"),
rw!("relu6_to_clamp"; "(relu6 ?x)" => "(clamp ?x)"),
rw!("relu6_to_act"; "(relu6 ?x)" => "(act ?x)")
]}
#[test]
fn duplicte_branch_select() {
let expr: RecExpr<NeuralNetwork> = "(+ (conv2d x) (conv2d (relu6 (conv2d x))))"
.parse()
.unwrap();
let mut egraph = EGraph::default();
egraph.add_expr(&expr);
egraph.dot().to_dot("target/pre.dot").unwrap();
let runner: Runner<NeuralNetwork, ()> = Runner::default().with_expr(&expr).run(&rules());
let extractor = Extractor::new(&runner.egraph, AstSize);
runner.egraph.dot().to_dot("target/graph.dot").unwrap();
let (best_cost, best_expr) = extractor.find_best(runner.roots[0]);
println!("End ({}):{}", best_cost, best_expr.pretty(80));
let mut egraph = EGraph::default();
egraph.add_expr(&best_expr);
egraph.dot().to_dot("target/post.dot").unwrap();
}
之前写过一篇带宽受限下的DSA后端优化, 不过主要是针对已经构建好Compute Schedule之后的优化, 今天准备展开讲讲. 从单层卷积到优化计算,再到Layer Fusion,以及后续各种优化,下面将通过一系列的例子来介绍:
首先需要实现高层IR的Index Mapping进行Infer Bounds, 这里我导入一个已经实现好的卷积的BoundsInfer.
from TracedArray import TarcedArray, GlobalHierarchy
from Conv2dBoundsInfer import Conv2dBoundsInfer, Segments
import torch
import numpy as np
Infer = Conv2dBoundsInfer(in_channels=2048, out_channels=512, kernel_size=1, groups=1, bias=True, padding=(
0, 0), stride=(1, 1), dilation=(1, 1), intput_shape=(1, 2048, 56, 56), test=False)假设我们的DSA有一个比较大的SRAM, 并且可以在这个SRAM上执行Tensor级别的操作, 约定好SRAM大小为L2SIZE. 这里引入GlobalHierarchy作为多级内存存储抽象,用于计算数据加载次数, 检查存储是否溢出. 那么考虑在上面编写一个最Navie的卷积. 为了匹配Tensor级别的计算操作, 我们将原本按1进行for循环执行的逻辑看作为按tile大小为1取tensor进行计算.
L2SIZE = 1536 * 1024 #
def demo1(imageArr: np.ndarray, weightArr: np.ndarray, outputArr: np.ndarray, targetOutput: np.ndarray):
image = TarcedArray(imageArr)
weight = TarcedArray(weightArr)
output = TarcedArray(outputArr)
(B, OC, OH, OW) = outputArr.shape
(tileB, tileOC, tileOH, tileOW) = (1, 1, 1, 1)
for b in Segments(0, B, tileB):
for oc in Segments(0, OC, tileOC):
for oh in Segments(0, OH, tileOH):
for ow in Segments(0, OW, tileOW):
with GlobalHierarchy(L2SIZE):
# 进入SRAM之后 从DDR中加在数据并计算.
outputTile = output[b, oc, oh, ow]
imageTile = image[Infer.get_input_segment(b, oc, oh, ow)]
weightTile = weight[Infer.get_w_segment(oc)]
outputTile += np.sum((imageTile * weightTile), keepdims=True)
assert (np.allclose(output._array, targetOutput, atol=1e-5))
print("demo1 total loaded :", GlobalHierarchy.TotalLoaded)
GlobalHierarchy.Reset()
demo1 total loaded : 6578274304可以发现我们重复加载了许多数据,也并没有加速计算, 但是实际上芯片中存在加速计算的硬件, 所以用以下方法来加速计算.
- SRAM有足够空间的情况下, 可以尝试一次计算更大的tensor,也就是选择更大的tile size. 比如把W上的tile size设置为最大, 把H上tile size加大.
- 假设我们有一个并行计算卷积部分输出的TensorCore, 一次最大并行输入16个input channel, 并行输出24个output channel.
接下来就可以来改造compute schedule:
CORE_OC = 24 # TensorCore并行限制
CORE_IC = 16
def TensorCore(image: np.ndarray, weight: np.ndarray) -> np.ndarray:
# 这里假设硬件可以自动循环
return torch.conv2d(torch.tensor(image), torch.tensor(weight)).numpy()
def demo2(imageArr: np.ndarray, weightArr: np.ndarray, outputArr: np.ndarray, targetOutput: np.ndarray):
image = TarcedArray(imageArr)
weight = TarcedArray(weightArr)
output = TarcedArray(outputArr)
(B, OC, OH, OW) = outputArr.shape
for b in Segments(0, B, 1):
for oc in Segments(0, OC, CORE_OC):
for oh in Segments(0, OH, 2):
for ow in Segments(0, OW, OW):
with GlobalHierarchy(L2SIZE):
outputTile = output[b, oc, oh, ow]
imageTile = image[Infer.get_input_segment(b, oc, oh, ow)]
weightTile = weight[Infer.get_w_segment(oc)]
outputTile += TensorCore(imageTile, weightTile)
assert (np.allclose(output._array, targetOutput, atol=1e-5))
print("demo2 total loaded :", GlobalHierarchy.TotalLoaded)
GlobalHierarchy.Reset()
demo2 total loaded : 179651584可以发现demo2减少了许多数据加载, 但从事高性能计算的朋友们应该可以发现对weight来说, 如果在OH/OW有切分, 那么在OH/OW循环内都是每次加载相同的weights[ic,kh,kw]. 那么我们就有两个选择来解决这个问题:
- 把weights加载的时机移动到OC循环内部或OC循环外部去加载, 这样在OH/OW的循环中可以不用load重复的weights了.
- 我们还可以增加OH/OW的tile size,然后再添加一个IC的切分维度, 这样每个循环也不会重复加载weights了, 但是值得注意的是此时output tile需要移动到oc循环内.
这里就是在SRAM中保存所有的weights, 实际上在stage到OC循环外之后, 我们还可以选择在OC循环内逐步的加载weights以进行流水.
def demo3_1(imageArr: np.ndarray, weightArr: np.ndarray, outputArr: np.ndarray, targetOutput: np.ndarray):
image = TarcedArray(imageArr)
weight = TarcedArray(weightArr)
output = TarcedArray(outputArr)
(B, OC, OH, OW) = outputArr.shape
for b in Segments(0, B, 1):
with GlobalHierarchy(L2SIZE):
reuse = False # 为了简单起见, 添加reuse的参数来避免重复统计load的数据, 其实应该把allocate buffer和load/store的逻辑分离出来.
weightTile = weight[Infer.get_w_segment(slice(0, OC))] # 将weights加载移动到OC循环外 也就是一次加载所有的权重
for oc in Segments(0, OC, CORE_OC):
for oh in Segments(0, OH, 2):
for ow in Segments(0, OW, OW):
outputTile = output[b, oc, oh, ow]
imageTile = image[Infer.get_input_segment(b, oc, oh, ow), reuse] # 重用同一份SRAM
if not reuse:
reuse = True
weightSubTile = weightTile[oc]
outputTile += TensorCore(imageTile, weightSubTile)
assert (np.allclose(output._array, targetOutput, atol=1e-5))
print("demo3-1 total loaded :", GlobalHierarchy.TotalLoaded)
GlobalHierarchy.Reset()
demo3-1 We can't move load weights statement out of OC!不过实际情况会发现因SRAM空间不够而出错. 这就是SRAM大小影响compute schedule.
把weights stage在OC循环内部, 这样可以在OH/OW循环中复用.
def demo3_2(imageArr: np.ndarray, weightArr: np.ndarray, outputArr: np.ndarray, targetOutput: np.ndarray):
image = TarcedArray(imageArr)
weight = TarcedArray(weightArr)
output = TarcedArray(outputArr)
(B, OC, OH, OW) = outputArr.shape
for b in Segments(0, B, 1):
for oc in Segments(0, OC, CORE_OC):
with GlobalHierarchy(L2SIZE):
reuse = False
weightTile = weight[Infer.get_w_segment(oc)]
for oh in Segments(0, OH, 2):
for ow in Segments(0, OW, OW):
outputTile = output[b, oc, oh, ow]
imageTile = image[Infer.get_input_segment(b, oc, oh, ow), reuse] # 重用同一份SRAM
if not reuse:
reuse = True
outputTile += TensorCore(imageTile, weightTile)
assert (np.allclose(output._array, targetOutput, atol=1e-5))
print("demo3-2 total loaded :", GlobalHierarchy.TotalLoaded)
GlobalHierarchy.Reset()
demo3-2 total loaded : 9586432虽然这个例子和demo3-1实际上差别不大, 但是主要是用于说明SRAM对于不同的Compute Schedule的限制.
注意这里我们添加一个IC的切分维度, 这样每次内部循环加载的就是不同的weights[oc,ic,:,:]的tile了.
def demo3_3(imageArr: np.ndarray, weightArr: np.ndarray, outputArr: np.ndarray, targetOutput: np.ndarray, prefix="demo3-3"):
image = TarcedArray(imageArr)
weight = TarcedArray(weightArr)
output = TarcedArray(outputArr)
(B, OC, OH, OW) = outputArr.shape
IC = imageArr.shape[1]
for b in Segments(0, B, 1):
for oc in Segments(0, OC, 8):
for oh in Segments(0, OH, OH):
for ow in Segments(0, OW, OW):
with GlobalHierarchy(L2SIZE):
reuse = False
outputTile = output[b, oc, oh, ow]
for ic in Segments(0, IC, CORE_IC):
wSeg = Infer.get_w_segment(oc)
wSeg[1] = ic # add slice in ic
weightTile = weight[wSeg, reuse]
imageSeg = Infer.get_input_segment(b, oc, oh, ow)
imageSeg[1] = ic # add slice in ic
imageTile = image[imageSeg, reuse]
outputTile += TensorCore(imageTile, weightTile)
if reuse is False:
reuse = True # reuse same buffer.
assert (np.allclose(output._array, targetOutput, atol=1e-5))
print(prefix, "total loaded :", GlobalHierarchy.TotalLoaded)
GlobalHierarchy.Reset()
demo3-3 total loaded : 4825088此时对于weights的加载比之前减少了一倍, 但是如果此时OH/OW有切分, 那么同一份ic的weights也会被多次加载. 而需要注意的是SRAM的大小有限, 所以必须缩小OC上的tile size, 来保证当前策略较优. 这就是tile size与SRAM大小共同影响compute schedule.
我们还可以尝试移动image stage到外层的循环, 因为每个oc内都加载了全部的input image, 那么将image移动到外层循环就可以减少许多重复的数据加载.
def demo4(imageArr: np.ndarray, weightArr: np.ndarray, outputArr: np.ndarray, targetOutput: np.ndarray):
image = TarcedArray(imageArr)
weight = TarcedArray(weightArr)
output = TarcedArray(outputArr)
(B, OC, OH, OW) = outputArr.shape
IC = imageArr.shape[1]
for b in Segments(0, B, 1):
with GlobalHierarchy(L2SIZE):
reuse = False
imageTile = image[Infer.get_input_segment(b, slice(0, OC), slice(0, OH), slice(0, OW))]
for oc in Segments(0, OC, 8):
for oh in Segments(0, OH, OH):
for ow in Segments(0, OW, OW):
outputTile = output[(b, oc, oh, ow), reuse]
for ic in Segments(0, IC, CORE_IC):
wSeg = Infer.get_w_segment(oc)
wSeg[1] = ic # add slice in ic
weightTile = weight[wSeg, reuse]
outputTile += TensorCore(imageTile[:, ic, :, :], weightTile)
if reuse is False:
reuse = True # reuse same buffer.
assert (np.allclose(output._array, targetOutput, atol=1e-5))
print("demo4 total loaded :", GlobalHierarchy.TotalLoaded)
GlobalHierarchy.Reset()
demo4 We can't move load image statement out of OC!但是很可惜这个卷积的image比较大, 如果所以移动到外循环会因为SRAM存不下而报错. 这就是compute schedule与不同的tile size可以相互影响的情况.
以上实验了单层卷积的情况, 我们尝试了调整tile size/调整buffer stage的位置来减少总的数据加载次数. 接下来我们需要考虑多个算子fusion的情况, 假设卷积前面不是一个带有reduction的算子, 比如binary add, 首先单独执行两个算子.
def demo5_1(imageArr: np.ndarray, biasArr: np.ndarray, weightArr: np.ndarray, outputArr: np.ndarray, targetOutput: np.ndarray):
image = TarcedArray(imageArr)
bias = TarcedArray(biasArr)
mid = TarcedArray(np.zeros_like(imageArr))
# binary add
(B, C, H, W) = imageArr.shape
for b in Segments(0, B, 1):
for c in Segments(0, C, 8):
for h in Segments(0, H, H):
for w in Segments(0, W, W):
with GlobalHierarchy(L2SIZE):
imageTile = image[b, c, h, w]
biasTile = bias[b, c, h, w]
midTile = mid[b, c, h, w]
midTile += imageTile + biasTile
demo3_3(mid._array, weightArr, outputArr, targetOutput, "demo5-1")
demo5-1 total loaded : 30515200那么每次算子执行结束后, 数据需要出DDR再回到SRAM, 这样就消耗了许多带宽.
我们可以发现,后面卷积的循环[B,OH,OW,IC]分别可以对应前面binary的[B,H,W,C], 其实即前面binary的H与W是可以依据卷积的tile size来确定, 他的C维度依据卷积的IC维度确定, 并且因为这个binary计算时没有元素依赖关系, 所以简单调整他的循环顺序我们就可以进行算子Fusion了, 也就是在IC的循环中计算elemwise的计算操作.
def demo5_2(imageArr: np.ndarray, biasArr: np.ndarray, weightArr: np.ndarray, outputArr: np.ndarray, targetOutput: np.ndarray):
image = TarcedArray(imageArr)
bias = TarcedArray(biasArr)
weight = TarcedArray(weightArr)
output = TarcedArray(outputArr)
(B, OC, OH, OW) = outputArr.shape
IC = imageArr.shape[1]
for b in Segments(0, B, 1):
for oc in Segments(0, OC, 8):
for oh in Segments(0, OH, OH):
for ow in Segments(0, OW, OW):
with GlobalHierarchy(L2SIZE):
reuse = False
outputTile = output[b, oc, oh, ow]
for ic in Segments(0, IC, CORE_IC):
wSeg = Infer.get_w_segment(oc)
wSeg[1] = ic # add slice in ic
weightTile = weight[wSeg, reuse]
imageSeg = Infer.get_input_segment(b, oc, oh, ow)
imageSeg[1] = ic # add slice in ic
imageTile = image[imageSeg, reuse]
biasTile = bias[imageSeg, reuse]
outputTile += TensorCore(imageTile + biasTile, weightTile)
if reuse is False:
reuse = True # reuse same buffer.
assert (np.allclose(output._array, targetOutput, atol=1e-5))
print("demo5-2 total loaded :", GlobalHierarchy.TotalLoaded)
GlobalHierarchy.Reset()
demo5-2 total loaded : 8036352可以发现减少了两倍的数据搬运.
首先测试两层卷积单独执行的数据加载.
def demo6(Infer1: Conv2dBoundsInfer, Infer2: Conv2dBoundsInfer, imageArr: np.ndarray, weightArr1: np.ndarray, weightArr2: np.ndarray, outputArr: np.ndarray, targetOutput: np.ndarray):
image = TarcedArray(imageArr)
weight1 = TarcedArray(weightArr1)
tempOutput = TarcedArray(np.zeros(Infer2.in_shape).astype(np.float32))
(B, OC, OH, OW) = Infer2.in_shape
with GlobalHierarchy(L2SIZE):
reuse = False
weight1Tile = weight1[:, :, :, :]
for b in Segments(0, B, 1):
for oc in Segments(0, OC, 16):
for oh in Segments(0, OH, 48):
for ow in Segments(0, OW, OW):
outputTile = tempOutput[(b, oc, oh, ow), reuse]
imageSeg = Infer1.get_input_segment(b, oc, oh, ow)
imageTile = image[imageSeg, reuse]
outputTile += TensorCore(imageTile, weight1Tile[oc])
if reuse is False:
reuse = True # reuse same buffer.
weight2 = TarcedArray(weightArr2)
output = TarcedArray(outputArr)
(B, OC, OH, OW) = outputArr.shape
with GlobalHierarchy(L2SIZE):
reuse = False
weight2Tile = weight2[:, :, :, :]
for b in Segments(0, B, 1):
for oc in Segments(0, OC, 16):
for oh in Segments(0, OH, 48):
for ow in Segments(0, OW, OW):
outputTile = output[(b, oc, oh, ow), reuse]
imageSeg = Infer2.get_input_segment(b, oc, oh, ow)
imageTile = tempOutput[imageSeg, reuse]
outputTile += TensorCore(imageTile, weight2Tile[oc])
if reuse is False:
reuse = True # reuse same buffer.
assert (np.allclose(output._array, targetOutput, atol=1e-5))
print("demo6 total loaded :", GlobalHierarchy.TotalLoaded)
GlobalHierarchy.Reset()
demo6 total loaded : 722528假设我们遇到前面一个算子是带有reduction的情况, 比如卷积+卷积. 那么只需要考虑将两层卷积的循环直接合并即可, 同时现在的compute schedule就不能和单层卷积时相同了, 在两层卷积的循环直接合并时, 我们无法在最后一层卷积的input channel上切分, 因为后一个卷积的每一份input channel都依赖前面一个卷积的所有input channel, 这样切分会导致前面的卷积的weights反复加载, 目前我实现的多层卷积的合并必须要在SRAM中可以存下所有的weights才可以.
def demo6_1(Infer1: Conv2dBoundsInfer, Infer2: Conv2dBoundsInfer, imageArr: np.ndarray, weightArr1: np.ndarray, weightArr2: np.ndarray, outputArr: np.ndarray, targetOutput: np.ndarray):
image = TarcedArray(imageArr)
weight1 = TarcedArray(weightArr1)
weight2 = TarcedArray(weightArr2)
output = TarcedArray(outputArr)
(B, OC, OH, OW) = outputArr.shape
IC = imageArr.shape[1]
with GlobalHierarchy(L2SIZE):
reuse = False
weight1Tile = weight1[:, :, :, :]
weight2Tile = weight2[:, :, :, :]
for b in Segments(0, B, 1):
for oc in Segments(0, OC, 16):
for oh in Segments(0, OH, 48):
for ow in Segments(0, OW, OW):
outputTile = output[(b, oc, oh, ow), reuse]
imageSeg2 = Infer2.get_input_segment(b, oc, oh, ow)
imageSeg1 = Infer1.get_input_segment(
imageSeg2[0], imageSeg2[1], imageSeg2[2], imageSeg2[3])
imageTile1 = image[imageSeg1, reuse]
imageTile2 = TensorCore(imageTile1, weight1Tile)
outputTile += TensorCore(imageTile2, weight2Tile[oc])
if reuse is False:
reuse = True # reuse same buffer.
assert (np.allclose(output._array, targetOutput, atol=1e-5))
print("demo6-1 total loaded :", GlobalHierarchy.TotalLoaded)
GlobalHierarchy.Reset()
demo6-1 total loaded : 206432宏观上, 我把一个Fused Layer内部计算(循环切分与buffer stage等)优化称为Compute Schedule, 而我之前的一篇文章在Fused Layer外部流水(buffer size search/ping pong buffer)优化称为Buffer Schedule. 我的理解是硬件架构决定了目前的Compute Schedule可能性, 接下来由软件来实现各种Compute Schedule Pattern, 后续再根据这些计算模式进行Buffer Schedule, 此时根据Buffer Schedule的结果来选择最优的Compute Schedule, 如此迭代才能尽量发挥硬件性能. 当然如果硬件架构给出的执行方式少, 那么对应的软件也简单, 否则硬件的灵活性大, 软件优化的难度也高. 整个系统的能力也就是软硬件协调程度的体现.
┌───────────────────────────────────────────────────────────────────────┐
│ │
│ │
│ ┌──────────────────────────────┐ │
│ │ │ │
│ │ │ │
┌───┴────┐ ┌───────┴────────┐ ┌───────▼───────┐ ┌────▼───┐
│Hardware├───────?Compute Schedule│ │Buffer Schedule├──────?Software│
└───▲────┘ └───────▲────────┘ └───────┬───────┘ └────┬───┘
│ │ │ │
│ │ │ │
│ └┘ │
│ │
└?┘微观上, 对于一个算子来说, 根据循环顺序/变量分配时机/切分方式的不同会导致显著的性能差距. 比如卷积, 为了尽量减少重复load weights可以在OC/IC进行切分. 同时如果考虑存储足够大还可以在不同循环维度去stage local buffer, 在内层循环里进行复用.
然后还有tile size search的优化, 上面的例子可能描述的不多, 但其实每种不同的计算模式还需要与之配套的tile search逻辑. 比如多层卷积fusion时需要尽量同时增大H和W来减少overlap还是先增大W保持连续的load; 单层卷积时先增大IC维度的tile还是OC维度的tile来满足内部TensorCore的利用率; 单层卷积是选择多占用一些SRAM来stream input还是增大一些OC/IC的tile来减少循环次数, 总之这套search tile size逻辑都需要和compute schedule以及硬件特性相匹配的.
接下来还有buffer schedule优化, 也就是多个tiled block之间, 开多少块buffer进行并行流水比较合适, 不同buffer数量时需要自动安排好每块buffer的生命周期, 内外循环都有ping pong时对于buffer正确访问, 硬件对于buffer的stride/shape限制, 代码展开的时候需要考虑软件流水, 最后还需要分析buffer读写依赖自动插入同步指令等. 最后假设如果search出来的tile size不合适, 比如切分的OC/IC太小硬件利用率不高, 那么可能还需要调整到别的compute schedule来重新走一遍上述流程.
如果是对于我上文描述的那样, 有很多种不同的计算方式可供选择, 那么对于手写算子来说就需要消耗许多的精力维护很多看似相同但是无法复用的逻辑, 所以需要有一种简单的DSL描述这些过程从而加速开发的迭代过程. 比如TVM TensorIR或exo-lang. 但感觉目前已有的技术还没法做到更自动化的Fusion, 因为多层Fusion的时候, 需要处理各种Index的变化, 比如DDR上的Tensor加载到SRAM之后不均匀切分, 每个循环所占据的SRAM Buffer大小并不一样, 并且对于卷积来说还有Padding的问题需要在SRAM中的Tile上处理好. DSL本身最好是可以将中间依赖关系以及index变换隐藏在其背后, 降低编写算子时需要记忆的内容, 并且对于多个手写的代码块可以做到自动的分析循环的依赖来进行Fusion.
我在实现自动Fusion的过程中也发现了不少问题:
- 缺乏分析循环间的依赖性的技术
我首先是构建了Tensor维度与循环依赖的表达式, 发现无法去分析循环间的依赖性, 比如DW卷积的OC维度就等于IC维度, Weights的IC维度此时依赖了OC维度, 而普通卷积的OC维度并不影响weights的IC维度, 因此就需要手动额外引入在IC维度上的TileVar.
2. 缺乏分析空间局部性的技术
如果可以直接从当前的Compute Schedule中发现如何移动循环或stage buffer可以减少数据重复加载, 那么可以指导Compute Schedule, 目前以上的优化方案还都是靠观察得到的.
3. 如何将硬件限制更好的描述到Fusion中
因为不同的case下总是需要为了兼容硬件bug/执行效率做出奇奇怪怪的修改. 比如我设计的规则是所有的L2上的Buffer按使用大小来申请, 但是由于硬件对于数据加载的速度问题, 有时候还需要申请更大的空间. 或者是硬件存在某种bug, 特定算子Fuse在一起时不能开启某些功能. 但是这些约束很难用一种通用的接口描述到自动生成的规则中. 只能在自动化的过程中hard code.
4. 如何更好将自动Fusion与手写算子结合
比如上面demo4的情况, 在SRAM有空余的时候, 我想在合适的地方stage image buffer, 对于手写算子来说可能就是移动几行代码的事情, 坐标变换就按当前的情况手写一个公式即可. 而自动优化为了通用还需要写许多的判断/转换.
最终就是各种硬件规则限制/性能优化trick的问题把原本规整的自动Fusion代码切分的支离破碎, 因为整套逻辑都通用, 每次都需要这一处改动还需要考虑是不是会对其他应用的地方产生额外的影响, 导致我花费了更多的精力, 算是让我体会到了worse is better. 不过也有可能是我实现的自动Fusion的功能太弱, 后续再学习一些多面体的知识看一下能否有帮助.





